М а т е р и а л ы X В с е р о с с и й с к о й н а у ч н о - п р а к т и ч е с к о й к о н ф е р е н ц и и
П о с в я щ а е т с я 1 0 0 - л е т и ю Р о с т и с л а в а Е в г е н ь е в и ч а А л е к с е е в а
663
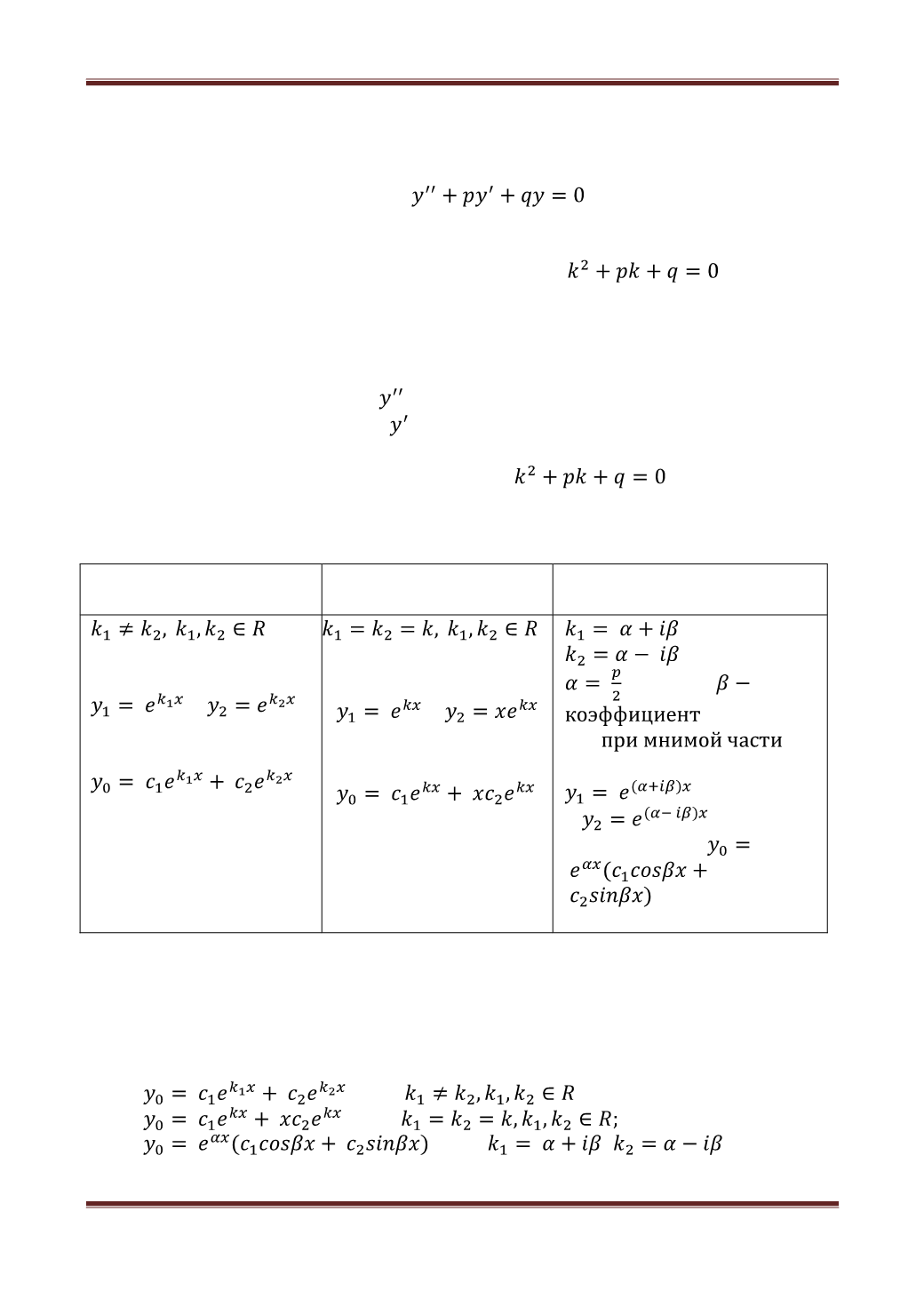
коэффициентами. Решение любого практического задания конструируется на
фундаменте теоретических знаний, в связи с этим изучение темы необходимо
начать с линейных однородных дифференциальных уравнений второго порядка
с постоянными коэффициентами
, где
p
и
q
– произвольные
действительные числа. Ключ к ответу кроется в отыскании корней квадратного
уравнения, которое ставит перед учащимися основную цель – первоначально
преобразовать уравнение в характеристическое
, которое и
будет являться квадратным. Чтобы приобрести умения по решению уравнений
такого рода, стоит подробно расписать план перехода от линейного
однородного дифференциального уравнения II порядка с постоянными
коэффициентами к характеристическому:
•
производим замену →
k
2
;
•
подставляем вместо в первоначальном уравнении
k
;
•
y
оставляем без изменений, то есть ничего не записываем.
С легкостью приходим к выводу:
– это обычное
квадратное уравнение, которое нужно решить. На данном этапе дальнейшие
действия по нахождению ответа зависят от коэффициентов p и q, как будут
найдены корни, можно столкнуться с тремя различными случаями:
Действительные
различные корни
Действительные
совпадающие корни
Корни – комплексно
сопряженная пара
,
частное решение
и
,
общее решение
;
,
частное решение
и
,
общее решение
;
,
, где
,
частное решение
и
,
общее решение
.
Познакомившись с теорией по данному виду линейного уравнения,
удобнее сделать небольшую шпаргалку для решения таких заданий –
последовательность выполнения действий:
1)
запись характеристического уравнения →2)нахождение его корней
→ 3)пользуясь заполненной выше таблицей, получение ответа:
, если
;
, если
, если
,
.
Закрепим теорию с помощью практических заданий.


