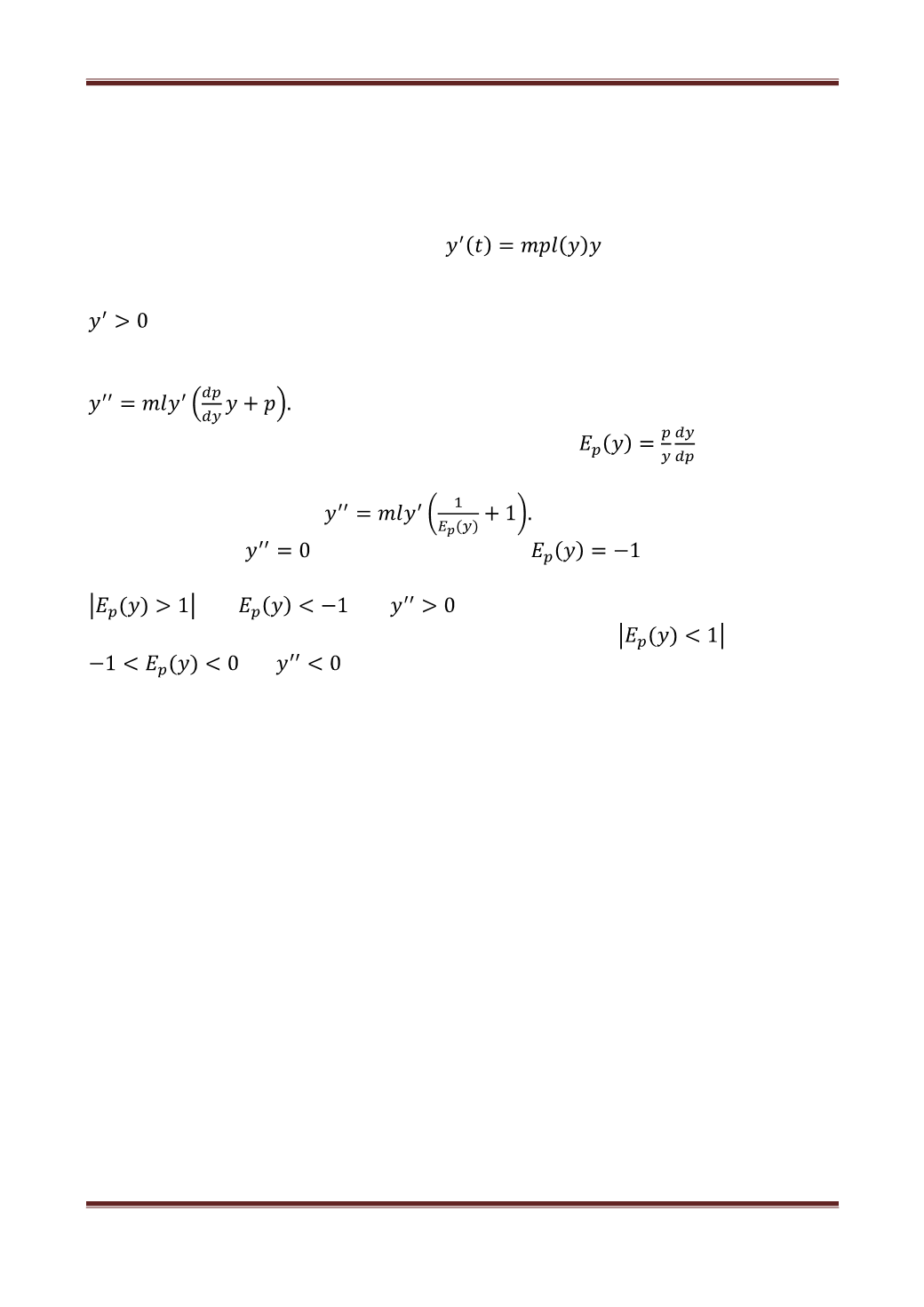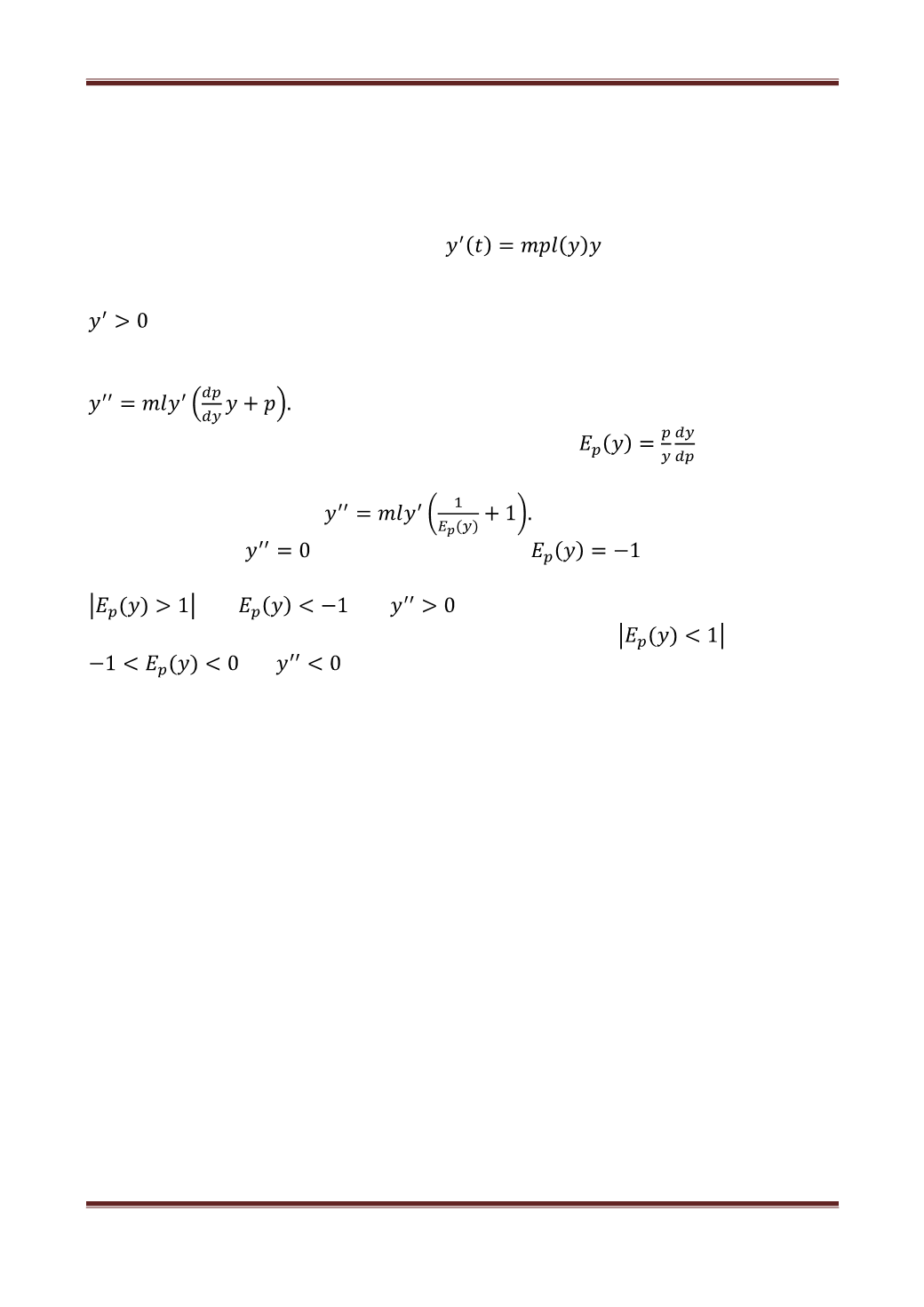
М а т е р и а л ы X В с е р о с с и й с к о й н а у ч н о - п р а к т и ч е с к о й к о н ф е р е н ц и и
П о с в я щ а е т с я 1 0 0 - л е т и ю Р о с т и с л а в а Е в г е н ь е в и ч а А л е к с е е в а
661
Но в действительности, данное условие насыщаемости рынка применимо
только в очень короткий промежуток. Поэтому, кривая спроса, т.е. зависимость
цены
р
проданноготовара от его объема
y
является убывающей функцией
p=p(y)
(с возрастанием объема произведенного товара его цена падает в результате
насыщения рынка). Таким образом, если рынок конкурентоспособен, то модель
роста будет задана уравнением вида
(9)
,
при этом она будет
оставаться уравнением с разделяющимися переменными.
Так как все множители в правой части уравнения (9) не отрицательны, то
, и это уравнение описывает функцию y(t),которая является
возрастающей на всем участке, а на выпуклость естественно используется
понятие эластичности функции. Действительно, из (9) следует, что
(10)
Эластичность спросаопределяется формулой
, относительно
цены. Тогда выражение (10) можно записать в виде
(11)
и условие
равносильно равенству
.
Таким образом, если спрос является эластичной функцией, т.е.
или
, то
и функция
y(t)
выпукла вниз; в случае,
если
спрос
неэластичен,
т.е.
,
или
, то
и функция
y(t)
выпукла вверх.
Когда решаем дифференциальные уравнения в частных производных,
обычно не стремимся найти общее решение, так как оно скорее всего будет
слишком общим, чтобы быть нам в чем-то полезным. Если решаем
обыкновенное дифференциальное уравнение и ответ определяется заданием
условий в одной или нескольких точках; то решая дифференциальное
уравнение в частных производных, ответ обычно задаетсяопределением
условий на одной или нескольких кривых. Дифференциальные уравнения
являются активным и нужным средством познания реальностисегодняшнего
мира. Они похожи на мгновенный снимок процесса в определенный момент
времени, интегрируя дифференциальное уравнение, мы по точным снимкам
восстанавливаем течение процесса в целом.
Библиографический список
1.
Веремеенко, Т.В. Высшая математика / Т.В. Веремееенко. – Минск:
ГИУСТ БГУ, 2002. – Ч.
2.
Кастрица, О.А. Высшая математика для экономистов / О.А.
Кастрица. – Минск: ООО Новое знание, 2006. – 490 с.
3.
Кремер, Н.Ш. Высшая математика для экономистов: Учебник для
вузов/ Н.Ш. Кремер. - М.: ЮНИТИ, 2003. - 471 с.