99
5.5.3. Одноканальная СМО с ограниченной длиной очереди
Рассмотрим простую одноканальную СМО с ограниченной очередью, в
которой число мест в очереди
m
– фиксированная величина. Следовательно, за-
явка, поступившая в тот момент, когда все места в очереди заняты, не принима-
ется к обслуживанию, не встает в очередь и покидает систему.
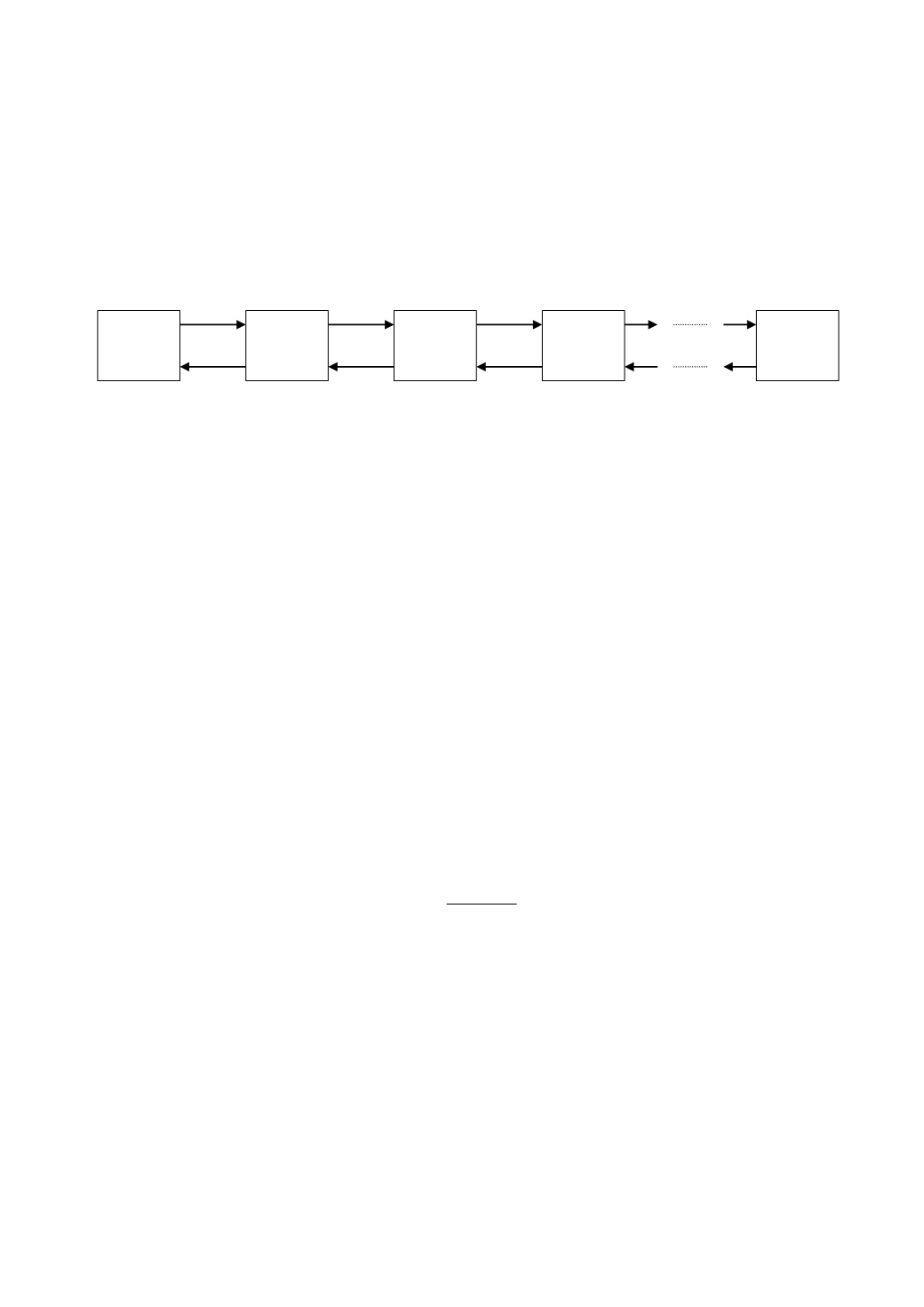
Граф этой СМО представлен на рис. 5.4.
Рис. 5.4. Размеченный граф процесса «рождения-гибели»
Состояния СМО можно представить следующим образом:
S
0
– канал обслуживания свободен,
S
1
– канал обслуживания занят, но очереди нет,
S
2
– канал обслуживания занят, в очереди стоит одна заявка,
S
3
– канал обслуживания занят, в очереди стоят две заявки,
……………………………………….
S
m
+1
– канал обслуживания занят, в очереди все
m
мест заняты, любая
следующая заявка получает отказ.
Для описания случайного процесса СМО можно воспользоваться изло-
женными ранее правилами и формулами. Напишем выражения, определяющие
предельные вероятности состояний:
Выражение для
p
0
можно в данном случае записать проще, пользуясь
тем, что в знаменателе стоит геометрическая прогрессия относительно
, тогда
после соответствующих преобразований получаем:
2
0
ρ
1
ρ
1
m
p
.
Эта формула справедлива для всех
, отличных от 1, если же
= 1, то
р
0
= 1/(
m
+ 2), а все остальные вероятности также равны 1/(
m
+ 2).
Определим основные характеристики одноканальной СМО с ожиданием:
относительную и абсолютную пропускную способность, вероятность отказа, а
также среднюю длину очереди и среднее время ожидания заявки в очереди.
Заявка получает отказ, если она поступает в момент времени, когда
СМО уже находится в состоянии
S
m
+1
и, следовательно, все места в очереди
m
заняты и один канал обслуживает. Поэтому вероятность отказа определяется
вероятностью появления состояния
S
m
+1
:
S
0
S
1
S
3
S
m
+1
S
2


