108
5.5.6. Многоканальная СМО с неограниченной очередью
Рассмотрим многоканальную СМО с ожиданием и неограниченной дли-
ной очереди, на которую поступает поток заявок с интенсивностью
и которая
имеет интенсивность обслуживания каждого канала
. Размеченный граф со-
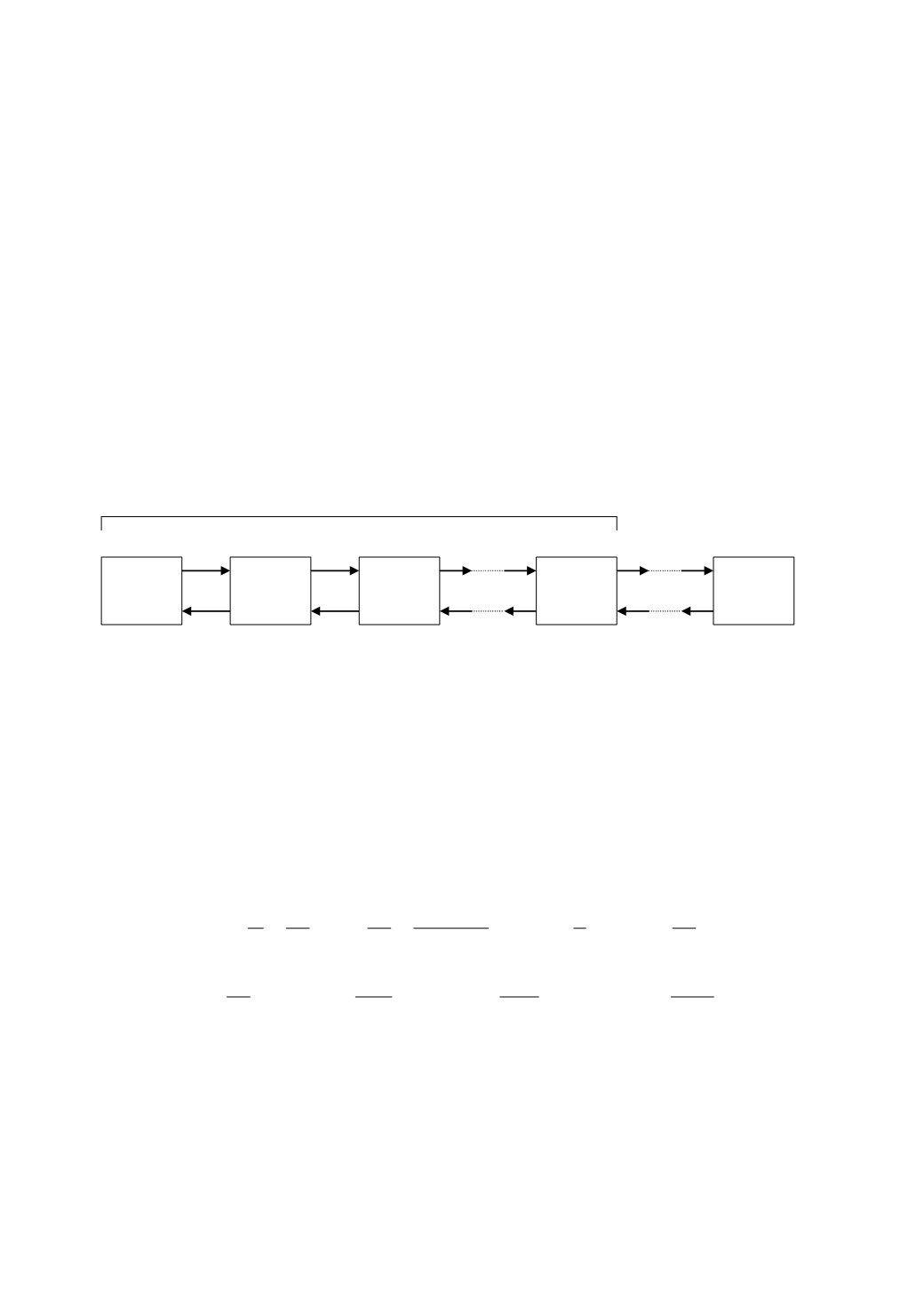
стояний представлен на рис. 5.7. Он имеет бесконечное число состояний:
S
0
–
все каналы свободны,
k =
0;
S
1
– занят один канал, остальные свободны,
k
= 1;
S
2
– заняты два канала, остальные свободны,
k
= 2;
………………………………………………………
S
n
– заняты все
n
каналов,
k
=
n
, очереди нет;
S
n+
1
– заняты все
n
каналов, одна заявка в очереди,
k
=
n
+ 1;
………………………………………………………
S
n+r
– заняты все
n
каналов,
r
заявок в очереди,
k
=
n
+
r
.
Рис. 5.7. Размеченный граф состояний многоканальной СМО
с неограниченной очередью
Вероятности состояний получим из формул для многоканальной СМО с
ограниченной очередью при переходе к пределу при
m
. Следует заметить,
что сумма геометрической прогрессии в выражении для
р
0
расходится при уровне
загрузки
/
n
1 (очередь будет бесконечно возрастать), а при
/
n <
1 ряд сходит-
ся, что определяет установившийся стационарный режим работы СМО, для кото-
рого и определим выражения для предельных вероятностей состояний:
;
!2
ρ
;
!1
ρ
;
!)
ρ
(
ρ
!
ρ
...
2!
ρ
1!
ρ
1
0
2
2 0
1
1
1
2
0
p
p p p
n n n
p
n
n
…;
.
!
...; ;
!
ρ
;
!
ρ
;
!
ρ
0
0 2
2
2
0
1
1
0
p
nn
p
p
n
n
p p
nn
p p
n
p
r
rn
rn
n
n
n
n
n
n
Поскольку отказа в обслуживании в таких системах не может быть, то
характеристики пропускной способности равны:
;
λ λ
;1 ;0
Q A
Q p
отк
среднее число заявок в очереди:
S
0
S
1
S
n
S
k
S
2
n
2
n
n
Очереди нет
3


