105
S
n
– заняты все
n
каналов,
k
=
n
.
Пока СМО находится в любом из этих состояний – очереди нет. После
того как заняты все каналы обслуживания, последующие заявки образуют оче-
редь, тем самым определяя дальнейшее состояние системы:
S
n
+1
– заняты все
n
каналов и одна заявка стоит в очереди,
k = n
+ 1,
S
n
+2
– заняты все
n
каналов и две заявки стоят в очереди,
k = n
+ 2,
……………………………………….
S
n+m
– заняты все
n
каналов и
m
мест в очереди,
k = n
+
m.
Граф состояний
n
-канальной СМО с очередью, ограниченной
m
места-
ми, представлен на рис. 5.6.
Переход СМО в состояние с большими номерами определяется потоком
поступающих заявок с интенсивностью
, тогда как по условию в обслужива-
нии этих заявок принимают участие
n
одинаковых каналов с интенсивностью
потока обслуживания равного
для каждого канала. При этом полная интен-
сивность потока обслуживания возрастает с подключением новых каналов
вплоть до такого состояния
S
n
, когда все
n
каналов окажутся занятыми. С появ-
лением очереди интенсивность обслуживания более не увеличивается, так как
она уже достигла максимального значения, равного
n
.
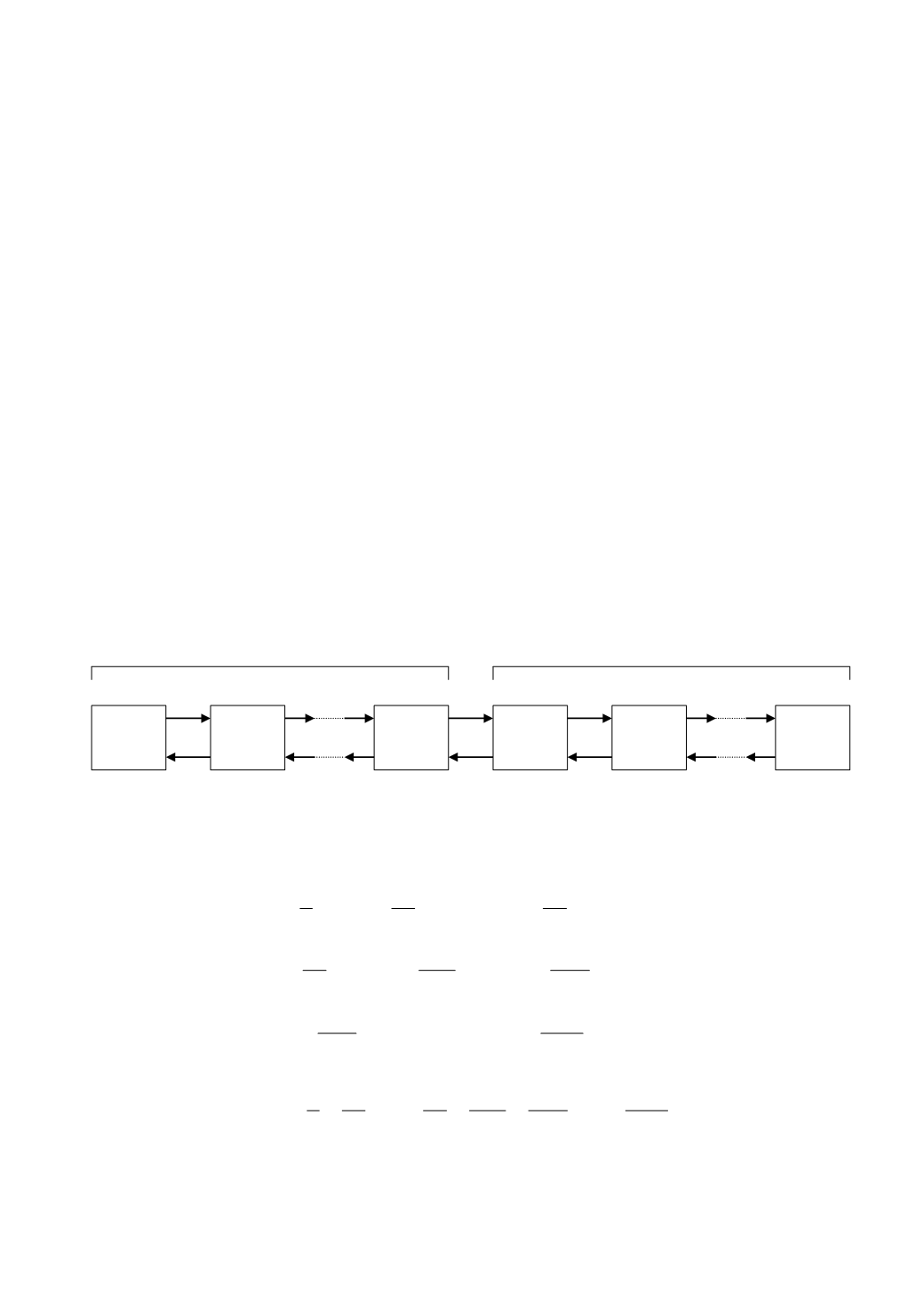
Рис. 5.6. Граф состояний
n
-канальной СМО с ограничением на длину очереди
m
Запишем выражения для предельных вероятностей состояний:
;
!
ρ
;
,
!
ρ
.........;
!
ρ
;
!
ρ
;
!
ρ
;
0,
!
ρ
.........;
!2
ρ
;
!1
ρ
0
0
0 2
2
2
0
1
1
0
0
0
2
2 0
1
отк
m
mn
mn
r
rn
rn
n
n
n
n
n
n
k
k
p p
nn
pmr np
nn
p
p
nn
pp
nn
pp
n
p
n k p
k
p
p
pp p
.
!
ρ
...
!
ρ
!
ρ
!
ρ
...
!2
ρ
!1
ρ
1
1
2
2
1
2
0
nn
nn nn n
p
m
mn
n
n
n
Образование очереди возможно, когда вновь поступившая заявка заста-
нет в системе не менее
n
требований, т.е. когда в системе будет находиться
n
,
S
0
S
1
S
n
+1
S
n+
2
S
n
n
2
n
n
S
n+m
n
n
Очереди нет
Очередь есть


