102
Такой режим работы СМО может явиться более предпочтительным по
сравнению с режимом работы при
= 1 потому, что ни одному из покупателей
не отказывается в обслуживании, хотя длина очереди и время обслуживания в
среднем несколько возрастают.
5.5.4. Одноканальная СМО с неограниченной очередью
Рассмотрим простейшую одноканальную СМО с ожиданием обслужи-
вания, на которую поступает пуассоновский поток заявок с интенсивностью
,
и интенсивностью обслуживания
. При этом заявка, поступившая в момент,
когда канал занят обслуживанием, ставится в очередь и ожидает обслуживания.
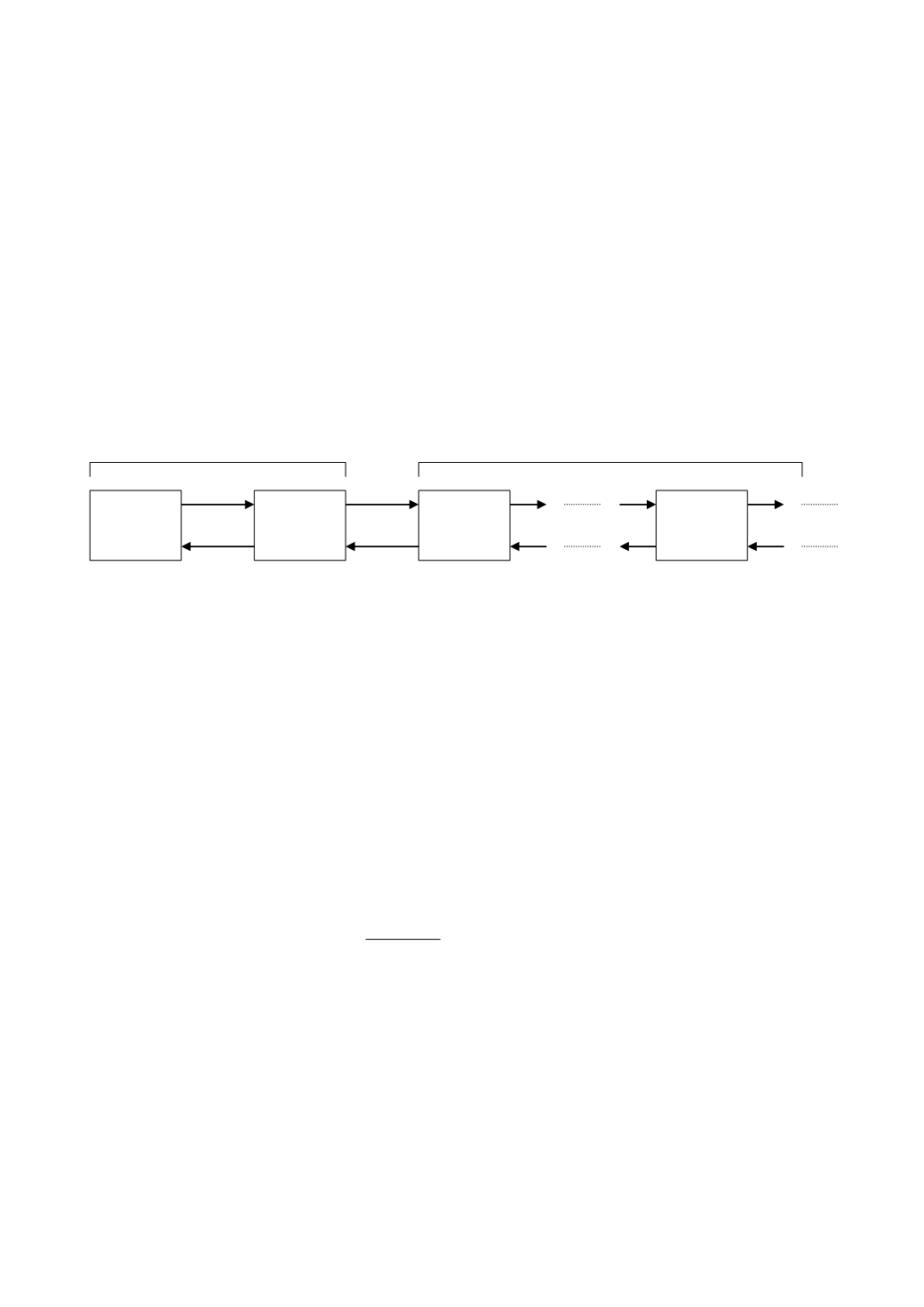
Размеченный граф состояний такой системы приведен на рис. 5.5.
Рис. 5.5. Размеченный граф одноканальной с неограниченной очередью
Количество возможных состояний ее бесконечно:
S
0
– канал обслуживания свободен, очереди нет,
k
=0,
S
1
– канал обслуживания занят, но очереди нет,
k
=1,
S
2
– канал обслуживания занят, в очереди стоит одна заявка,
k
=2,
……………………………………….
S
k
– канал обслуживания занят (
k
– 1), заявка в очереди.
Модели оценки вероятности состояний СМО с неограниченной очере-
дью можно получить из формул, выведенных для СМО с ограниченной очере-
дью, путем перехода к пределу при
m
:
.......
.........
),
ρ
1(
ρ
......,
.........
,
ρ)
(1
ρ
),
ρ
1(
ρ
,
ρ
1
.......
.........
,
ρ
......,
.........
,
ρ
,
ρ
,
1
ρ
1
2
2
1
0
0
0
2
2
0
1
2
0
k
k
k
k
m
p
p
p
p
p
p
p p
p p
p
Поскольку в рассматриваемой СМО ограничение на длину очереди от-
сутствует, то любая заявка может быть обслужена, поэтому
р
обс
= 1, следова-
S
0
S
2
S
k
S
1
Очереди нет
Очередь любой длины


