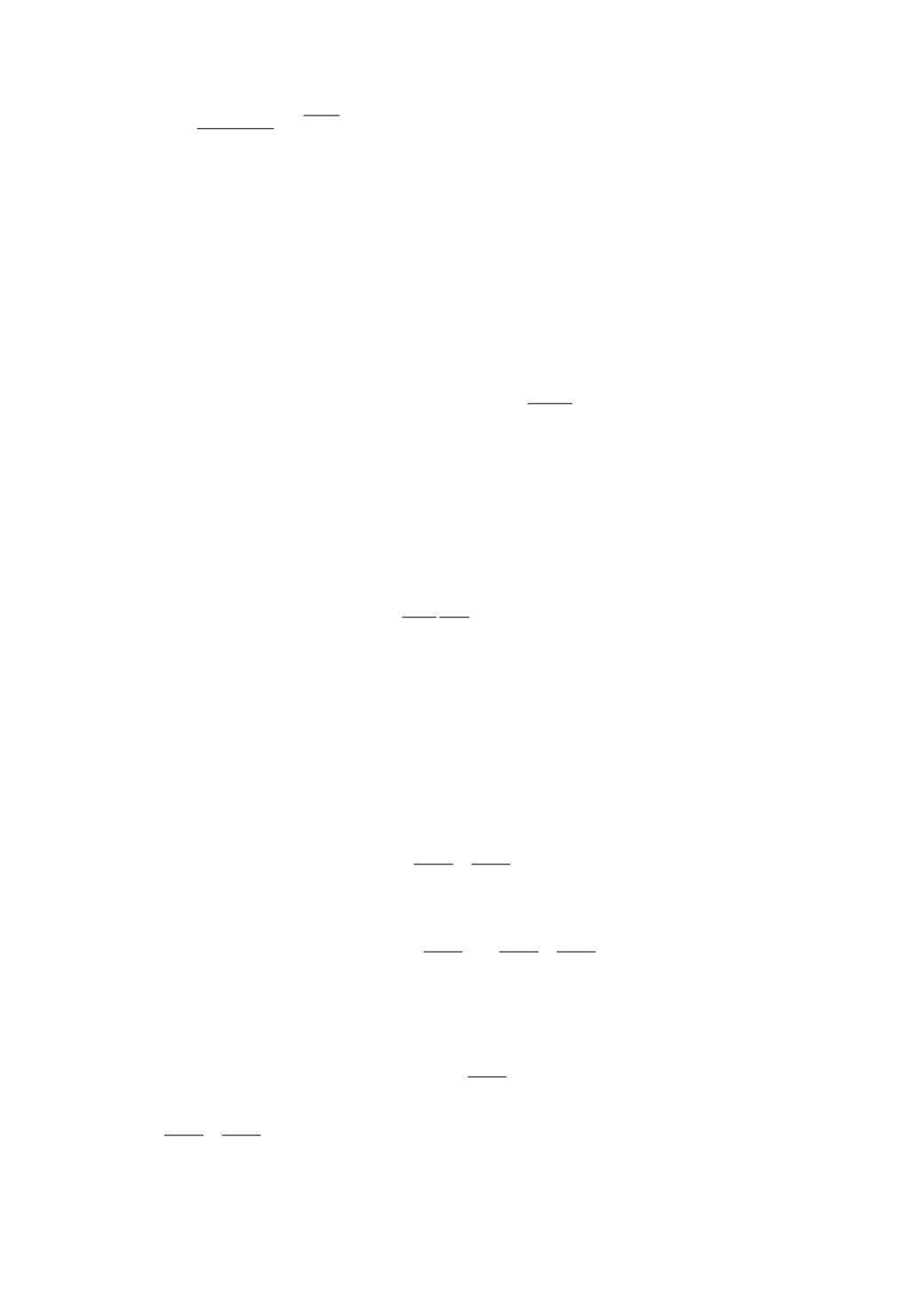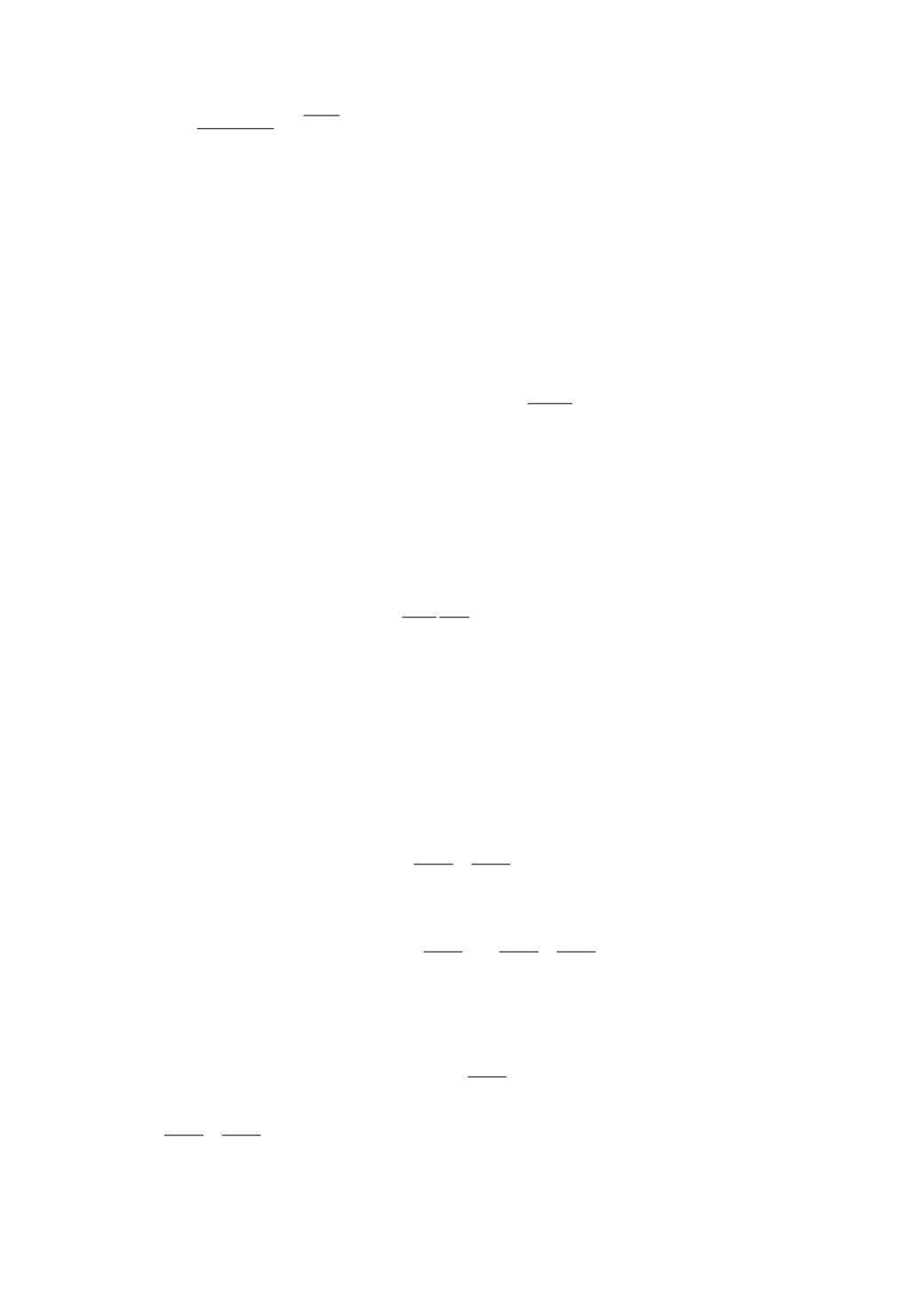
175
нечетное,
,
0
четное,
,
1
2
1
)1(1
1
1
1
k
k
k
k
dt t
k
k
заключаем, что для решения поставленной задачи достаточно определить
i
t
и
i
A
из системы 2
n
уравнений
n
i
n
i i
n
i
n
i i
n
i
i i
n
i
i
t
A
n
tA
tA
A
1
1 2
1
2 2
1
1
.0
,
1 2
2
...
,0
,2
(6.9)
Система (6.9)
нелинейная и исследование ее громоздко. Поэтому
чтобы упростить решение в качестве узлов
i
t
берут корни полинома
Лежандра
n
-й степени:
.)..,2
,1,0 (
1
! 2
1
)
(
2
n
x
dx
d
n
xP
n
n
n
n
n
. (6.10)
Формула (6.7), где
i
t
– нули полинома Лежандра
)
(
t
P
n
и
) ...,3,2,1 (
n
i A
i
определяются из системы (6.9), называется
квадратурной
формулой Гаусса
.
Рассмотрим использование квадратурной формулы Гаусса для
вычисления общего интеграла
b
a
dxxf
)
(
. Делаем замену переменной
t
ab ba
x
2
2
.
(6.11)
Получим
dt t
ab ab
f
ab
dxxf
b
a
1
1
2
2
2
)
(
.
(6.12)
Применяя к интегралу (6.12) квадратурную формулу Гаусса (6.7), будем
иметь
n
i
i
i
b
a
xfA
ab
dxxf
1
) (
2
)(
,
(6.13)
где
)
,
...,2,1 (
2
2
n
i
t
ab ba
x
i
i
;
i
t
– нули полинома Лежандра
)(
tP
n
.