173
относительно
n
:
ε
n
R
, где
n
R
– остаточный член; а
– необходимая
точность вычисления. После этого вычислить интеграл, используя
n
точек
разбиения.
Остаточный член для метода левых прямоугольников
)('
2
)
(
2
c f
n
ab
R
n
,
где
)
('
c f
имеет максимальное значение на
]
,
[
ba
.
Остаточный член для метода правых прямоугольников
)
('
2
)
(
2
c f
n
ab
R
n
,
где
)
('
c f
имеет максимальное значение на
]
,
[
ba
.
Остаточный член для метода средних прямоугольников
)(
24
)
(
2
3
c f
n
ab
R
n
,
где
)(
c
f
имеет максимальное значение на
] ,[
ba
.
Остаточный член для метода трапеций
)(
12
)
(
2
3
c
f
n
ab
R
n
,
где
)(
c
f
имеет максимальное значение на
] ,[
ba
.
Остаточный член для метода Симпсона
)(
180
)
(
) (
4
5
c f
n
ab
R
IV
n
,
где
)
(
) (
c f
IV
имеет максимальное значение на
]
,
[
ba
.
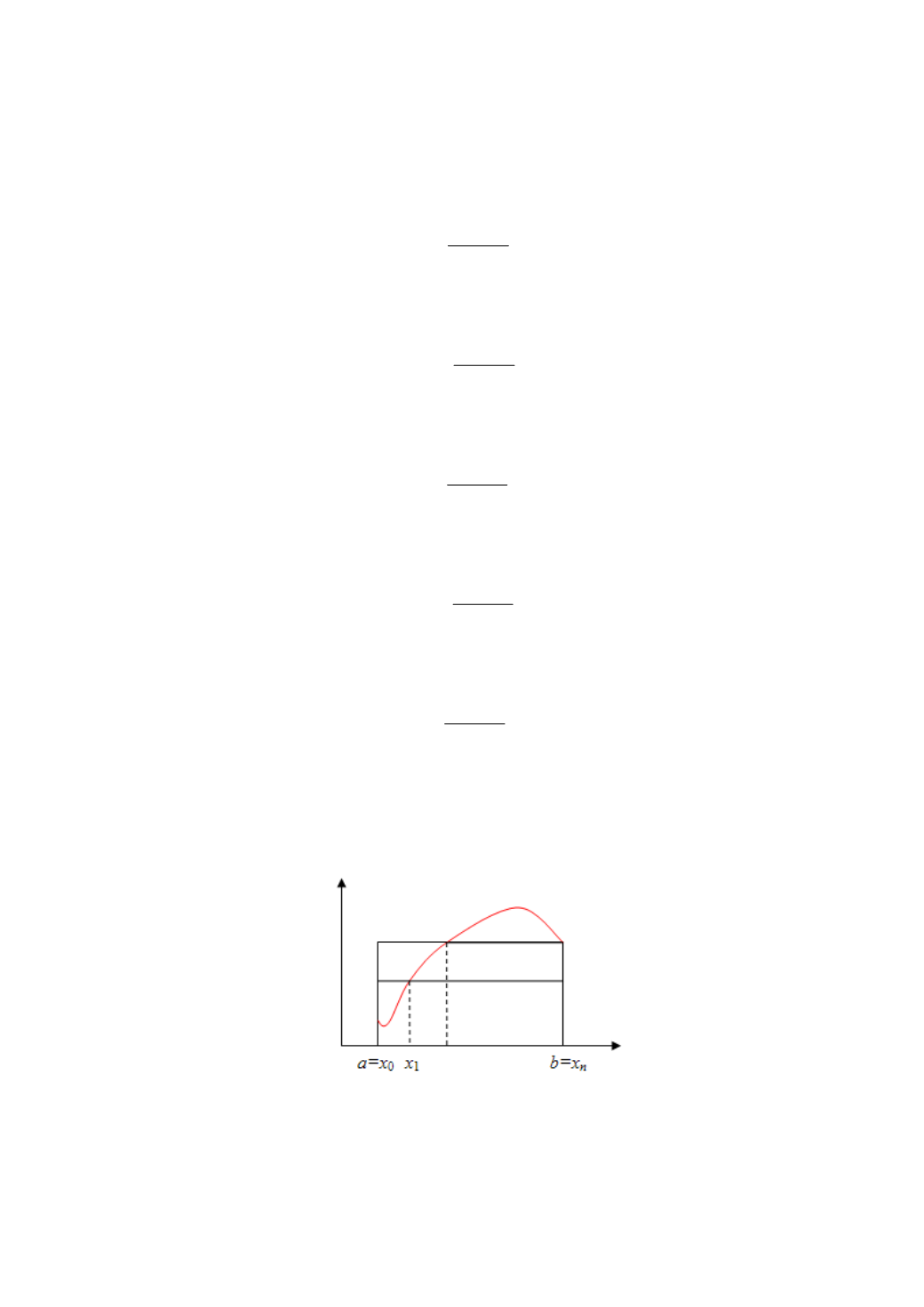
6.9. Метод Монте-Карло. Реализация простого метода
Рис. 6.6. Метод Монте-Карло
Данный способ можно также интерпретировать как статистический
вариант метода прямоугольников, когда в качестве узла
i
x
берется


