170
1
1
0
) (
2
) ( ) (
)(
n
i
i
n
b
a
xf
xf
xf
h dxxf
.
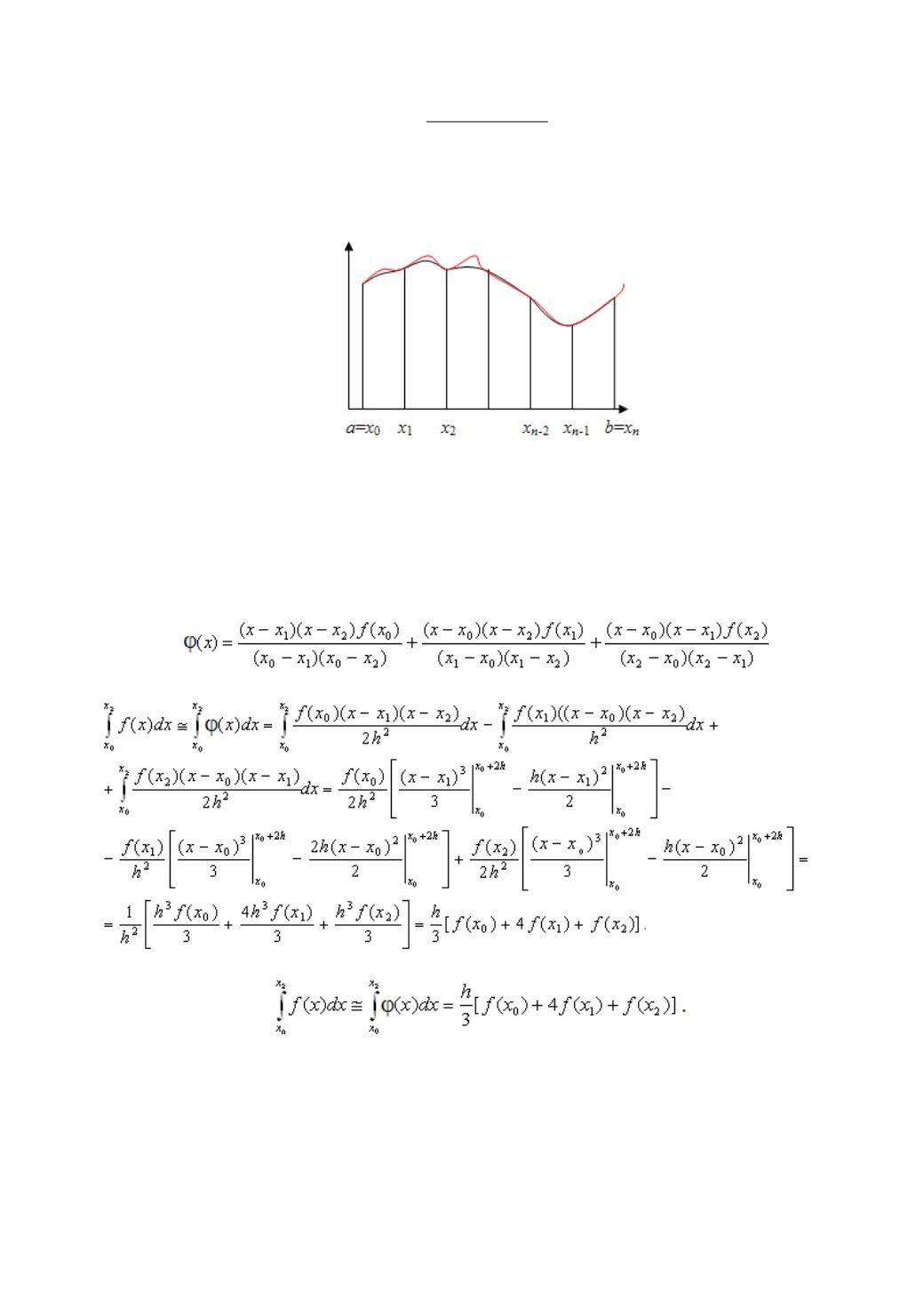
6.6. Метод Симпсона (парабол)
Рис. 6.5. Графическая реализация метода Симпсона (парабол)
Метод основан на аппроксимации функции
f
(
x
) на каждом частичном
интервале
1 1
;
i
i
x x
(количество частичных отрезков
i
i
x
x
;
1
должно быть
четным) многочленом Лагранжа второй степени
2
2
1
0
xaxa a y
i
, т.е.
параболой. Он имеет вид
.
Проинтегрируем
(
x
)
Таким образом, получим
Оценим теперь погрешность интегрирования по формуле Симпсона.
Будем считать, что у
f
на отрезке
]
2
, [
0 0
h
x
x
существуют непрерывные
производные
'
'
'' ,'
'
' ,
'
'
,
'
f
f
f f
. Составим разность


