169
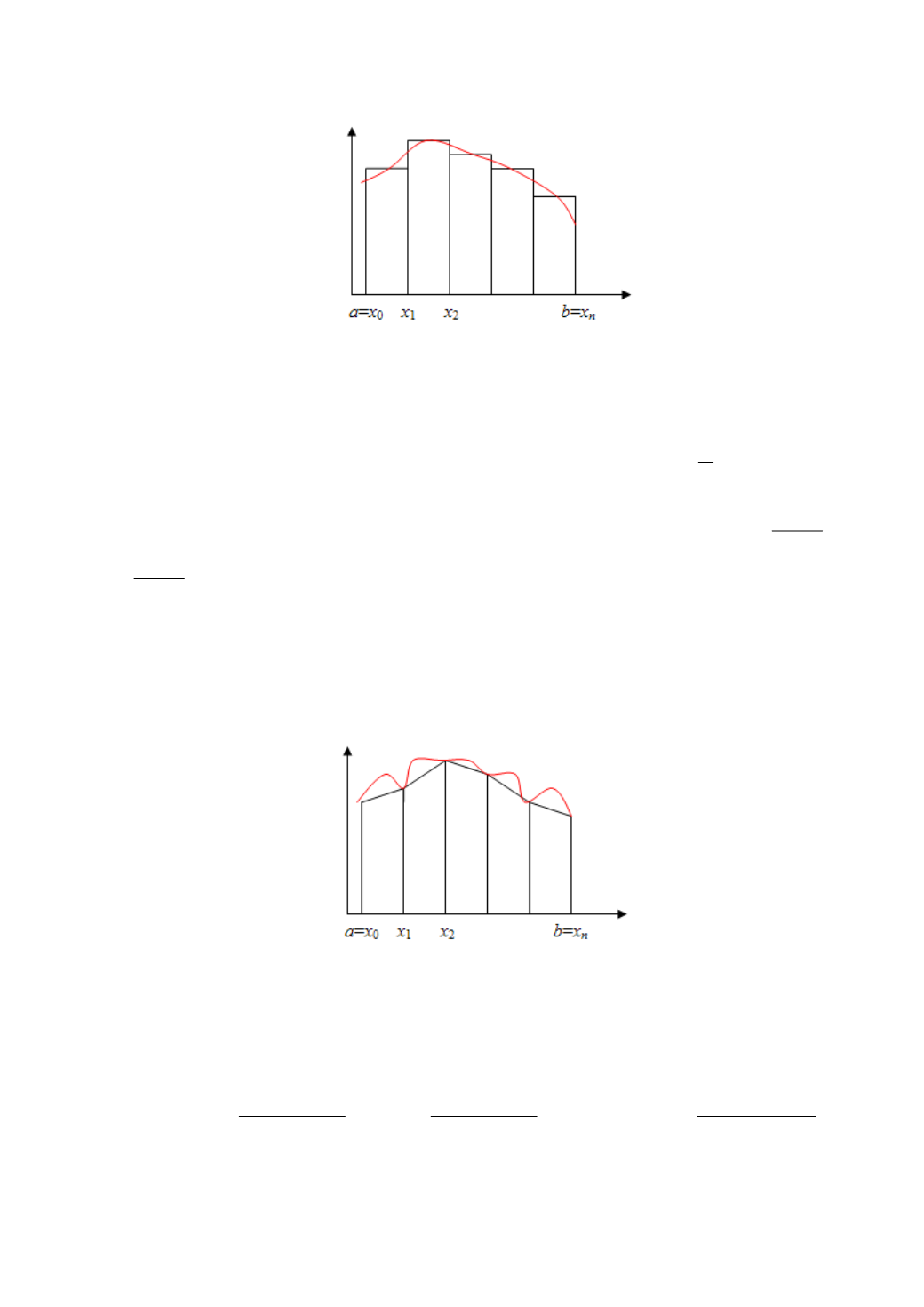
6.4. Метод средних прямоугольников
Рис. 6.3. Графическая реализация метода средних прямоугольников
Метод основан на аппроксимации функции
f
(
x
) на каждом частичном
интервале
1
;
i
i
xx
многочленом Лагранжа нулевой степени
const
0
2
1
a y
i
.
Другими словами, для нахождения значения интеграла необходимо найти
среднее значение
х
, используя каждые две соседние точки
2
1 0
1
x x
x
c
,
2
2
1
2
x x
x
c
и т.д., определить площади
h
x
f
S
c
) (
1
1
,
h
x
f
S
c
) (
2
2
, …
h
x
f
S
cn
n
) (
(рис. 6.3) и сложить их.
)] (
...
) ( ) ( [
)(
1
0
cn
c
c
b
a
xf
xf
xfh dxxf
.
6.5. Метод трапеций
Рис. 6.4. Графическая реализация метода трапеций
Метод основан на аппроксимации функции
f
(
x
) на каждом частичном
интервале
1
;
i
i
xx
многочленом Лагранжа первой степени
x
a
a
y
i
1
0
.
Другими словами, для нахождения значения интеграла необходимо найти
площади
h
x
f
x
f
S
2
) ( ) (
1
0
1
,
h
x
f
xf
S
2
) ( ) (
2
1
2
, …,
h
xf
xf
S
n
n
n
2
)
(
)
(
1
(рис. 6.4), равные площадям получившихся трапеций, и сложить их.


