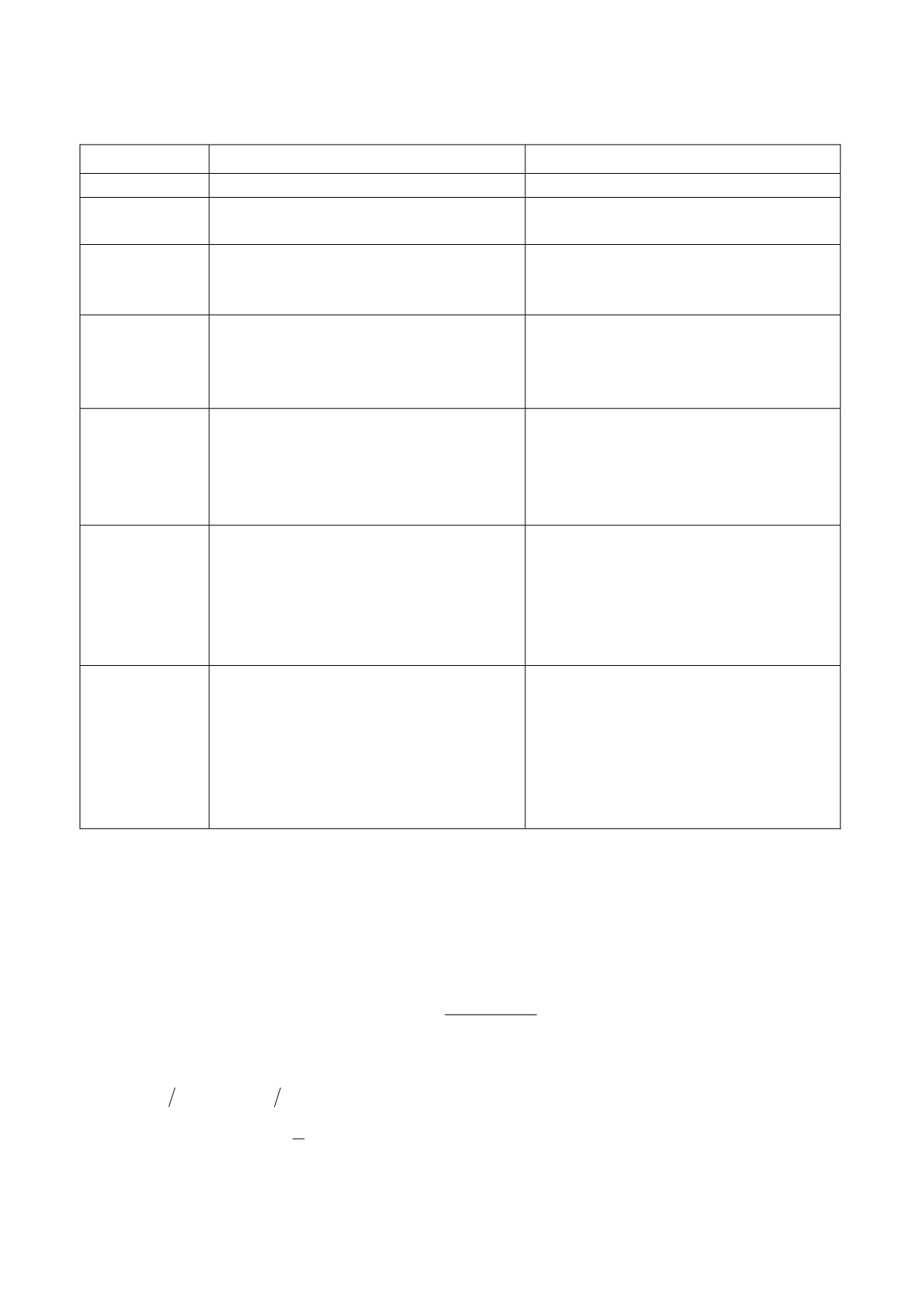
176
Таблица 6.2
Таблица узлов и коэффициентов формулы Гаусса
n
i
t
i
A
1
t
1
=0
A
1
=2
2
t
1
=0,577350269
t
2
=-0,577350269
A
1
=1
A
2
=1
3
t
1
=0,774596669
t
2
=0
t
3
=0,774596669
A
1
=0,555555556
A
2
=0,888888889
A
3
=0,555555556
4
t
1
=-0,861136312
t
2
=-0,339981044
t
3
=0,339981044
t
4
=0,861136312
A
1
=0,347854845
A
2
=0,652145155
A
3
=0,652145155
A
4
=0,347854845
5
t
1
=-0,906179846
t
2
=-0,538469319
t
3
=0
t
4
=0,538469319
t
5
=0,906179846
A
1
=0,236929885
A
2
=0,478628670
A
3
=0,56888889
A
4
=0,478628670
A
5
=0,236929885
6
t
1
=-0,932469514
t
2
=-0,661209386
t
3
=-0,238619186
t
4
=0,238619186
t
5
=0,661209386
t
6
=0,932469514
A
1
=0,171324492
A
2
=0,360761573
A
3
=0,467913934
A
4
=0,467913934
A
5
=0,360761573
A
6
=0,171324492
7
t
1
=-0,949107912
t
2
=-0,741531185
t
3
=-0,405845151
t
4
=0
t
5
=0,405845151
t
6
=0,741531185
t
7
=0,949107912
A
1
=0,129484966
A
2
=0,279705391
A
3
=0,381830051
A
4
=0,417959184
A
5
=0,381830051
A
6
=0,279705391
A
7
=0,129484966
6.11. Примеры
Пример 6.1
Вычислить интеграл
I
по формуле Симпсона при
n
= 8, оценить
остаточный член формулы, составив таблицу конечных разностей:
6,1
2,1
2
.
1
1,2 2 sin
dx
x
x
I
Решение.
Согласно
условию,
n
=
8,
поэтому
.05,082,1
6,1
na
b
h
Вычислительная формула имеет вид
,
4 2 4 2 4 2 4
3
8
7
6
5
4
3
2
1
0
y y y y y y y y y
h
I


