179
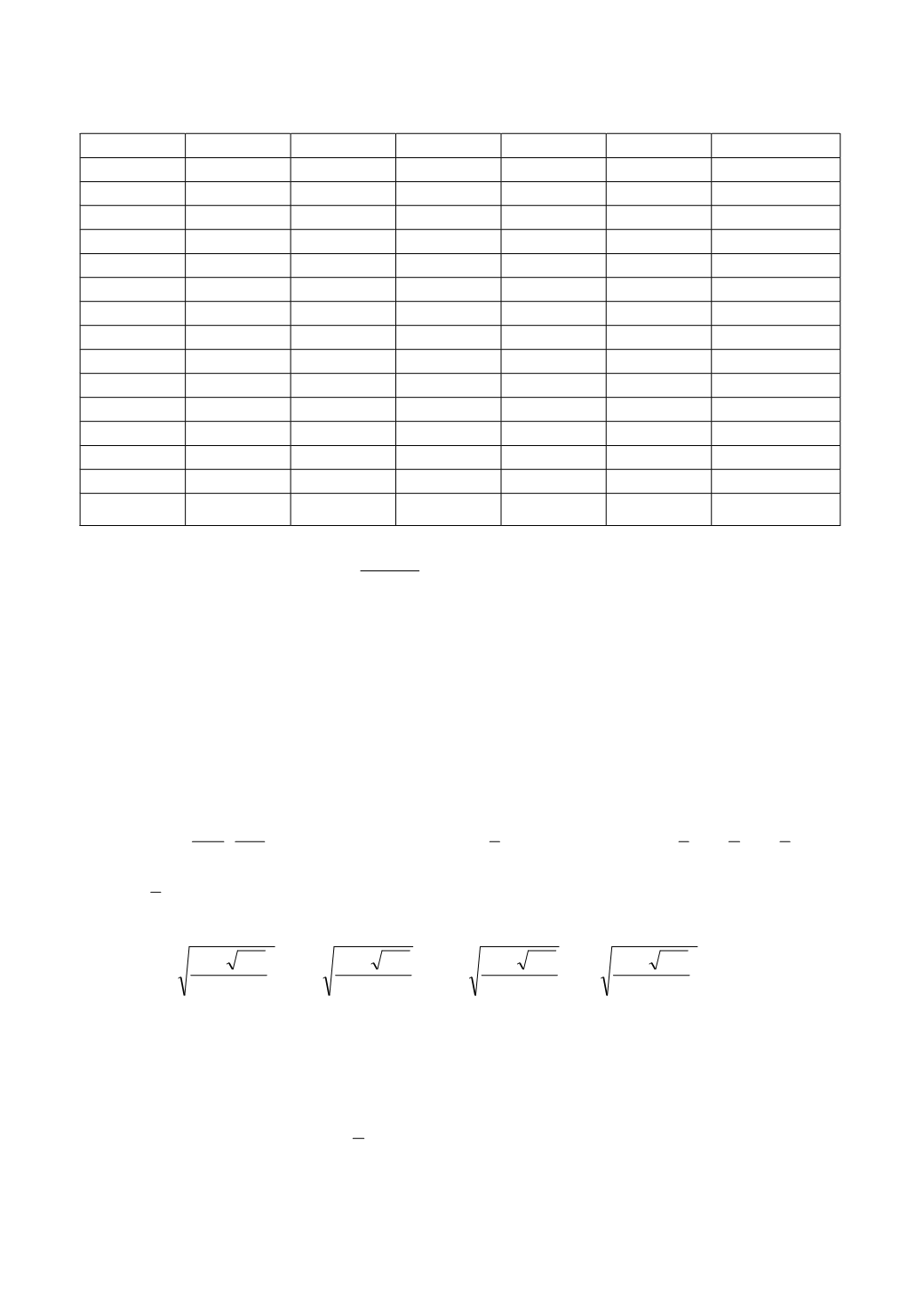
Окончание табл. 6.5
1
2
3
4
5
6
7
7
0,91
0,8281
1,9562
1,3986
0,71501
8
0,94
0,8836
2,0672
1,4378
0,69551
9
0,97
0,9409
2,1818
1,4771
0,67700
10
1,00
1,0000
2,3000
1,5166
0,65937
11
1,03
1,0609
2,4218
1,5562
0,64259
12
1,06
1,1236
2,5472
1,5960
0,62657
13
1,09
1,1881
2,6762
1,6356
0,61140
14
1,12
1,2544
2,8088
1,6759
0,59669
15
1,15
1,3225
2,9450
1,7161
0,58272
16
1,18
1,3924
3,0848
1,7564
0,56935
17
1,21
1,4641
3,2282
1,7967
0,55658
18
1,24
1,5376
3,3752
1,8372
0,54431
19
1,27
1,6129
3,5258
1,8777
0,53253
20
1,30
1,6900
3,6800
1,9817
0,52129
0,
1,40515
12,77022
Таким образом,
404 ,0
40418 ,0
77022 ,12
2
40515 ,1
03
,0
I
.
Ответ:
. 404 ,0
I
Пример 6.3
Найти точки
i
x
и коэффициенты
i
A
для
4
n
для квадратуры Гаусса и
вычислить интеграл
1
1
)1 (
dx x
.
Решение. Полином Лежандра четвертой степени
.)3 30
35(
8
1
8
3
8
6
8
3
3 4 )1 (
8
3
)1 (3
)1
(
!42
1
)(
2
4
2
4
2
4
2
2
2
2
4
4
2
4
4
4
4
x
x
x
x
x x
x
x x
x
x
dx
d
tP
Приравнивая этот полином к нулю, находим корни:
,
35
120
15
,
35
120
15
,
35
120
15
,
35
120
15
4
3
2
1
t
t
t
t
.
861136312
,0
,
339981044
,0
,
339981044
,0
,
861136312
,0
4
3
2
1
t
t
t
t
Для определения коэффициентов
A
1
,
A
2
,
A
3
,
A
4
имеем систему
.0
,
3
2
,0
,2
4
3
4 3
3
3 2
3
2 1
3
1
4
2
4 3
2
3 2
2
2 1
2
1
4 4 3 3 2 2 1 1
4
3
2
1
At At At At
At At A
t
At
At At At At
A A A A


