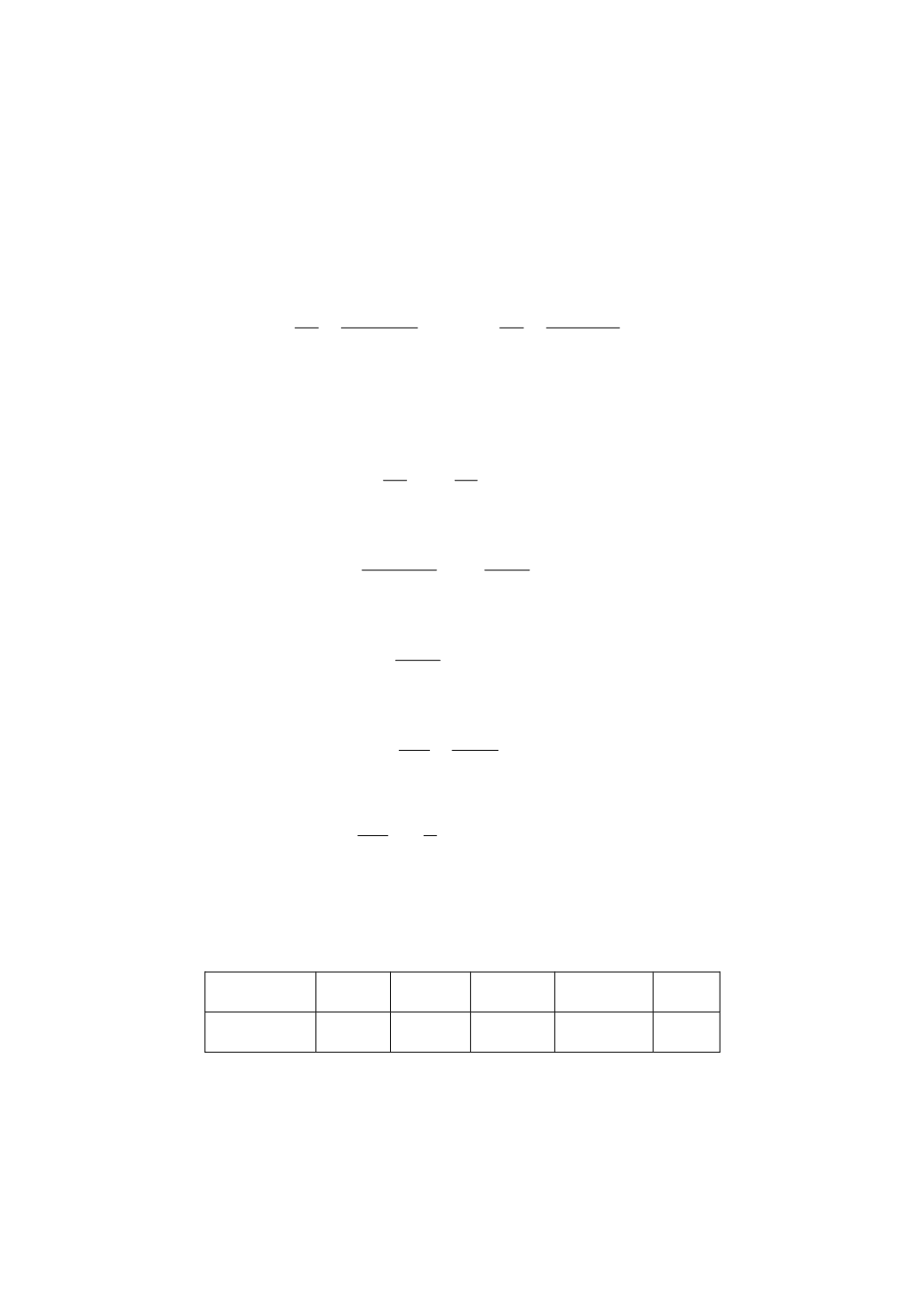
111
служивания
Т
обс
меньше числа обслуживающих каналов. Это обусловлено вероят-
ностным характером как потока заявок, так и временем их обслуживания. Поэто-
му о рациональности варианта организации СМО можно рассуждать лишь в том
случае, если
n
>
. Поскольку из условия задачи следует, что интенсивность
нагрузки
=
/
= 2, то вычисления показателей системы следует начать с
n
= 3.
Сначала определяем долю времени простоя контролеров-кассиров в те-
чение рабочего дня, т.е. при условии отсутствия покупателей:
.11,0
)23(!3
2
!
2
)
ρ
(!
ρ
!
ρ
1
3
0
13
1
0
1
0
k
k
n
k
n
k
k
nn k
p
Следовательно, три контролера-кассира будут простаивать 11% времени
от всей продолжительности рабочего дня. В результате получим следующее:
вероятность застать всех контролеров-кассиров занятыми:
; 148 ,0 11,0
!3
2
!
ρ
3
0
p
n
p
n
n
вероятность оказаться в очереди:
; 445 ,0
ρ
!)
ρ
(
ρ
0
n
n
оч
p
n
n
p
n n
n
p
среднее число покупателей, находящихся в очереди:
чел; 523,1
ρ
оч
оч
p
n
n
L
среднее время ожидания покупателями в очереди начала обслуживания:
; 617 ,0
2
235
,1
λ
оч
оч
L
T
относительная величина затрат для
n =
3 и
С
оч
= З
С
K
составляет:
.
351
,3 3
λ
1
оч
K
T n
C
C
Затем проводим аналогичные вычисления по определению перечисленных
показателей для других значений
n
= 4, 5, 6 и результаты запишем в табл. 5.2.
Таблица 5.2
n
3
4
5
6
7
C
/
C
K
3,351 2,525
2,65
3,04
3,512
По данным таблицы следует, что оптимальное число контролеров-
кассиров в узле расчета
n
0
= 4 для соотношения
С
оч
/
С
K
= 3/1. при этом общие за-
траты будут минимальными. Аналогичную задачу можно решить, задав другие
соотношения
С
оч
/
С
K
.


