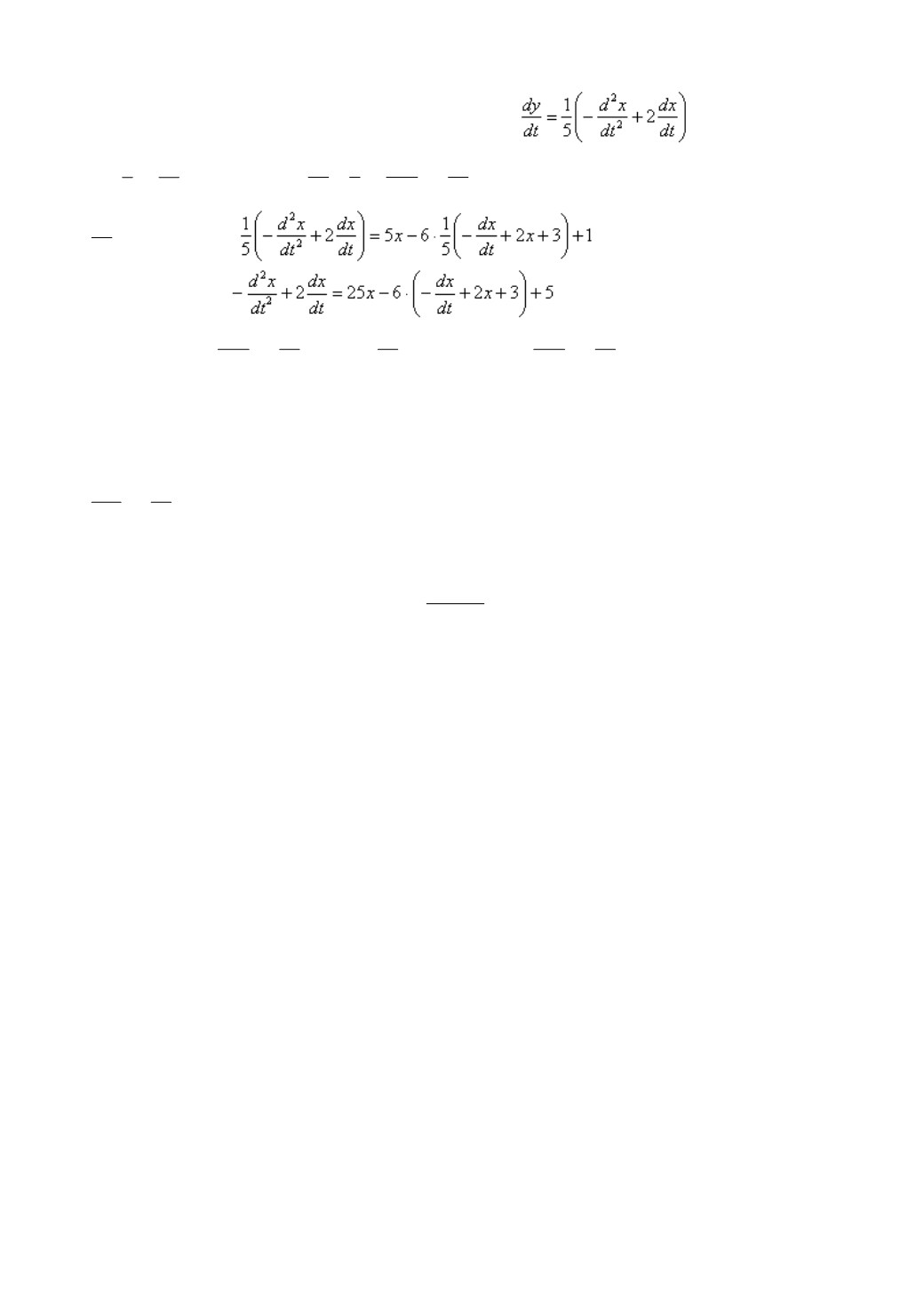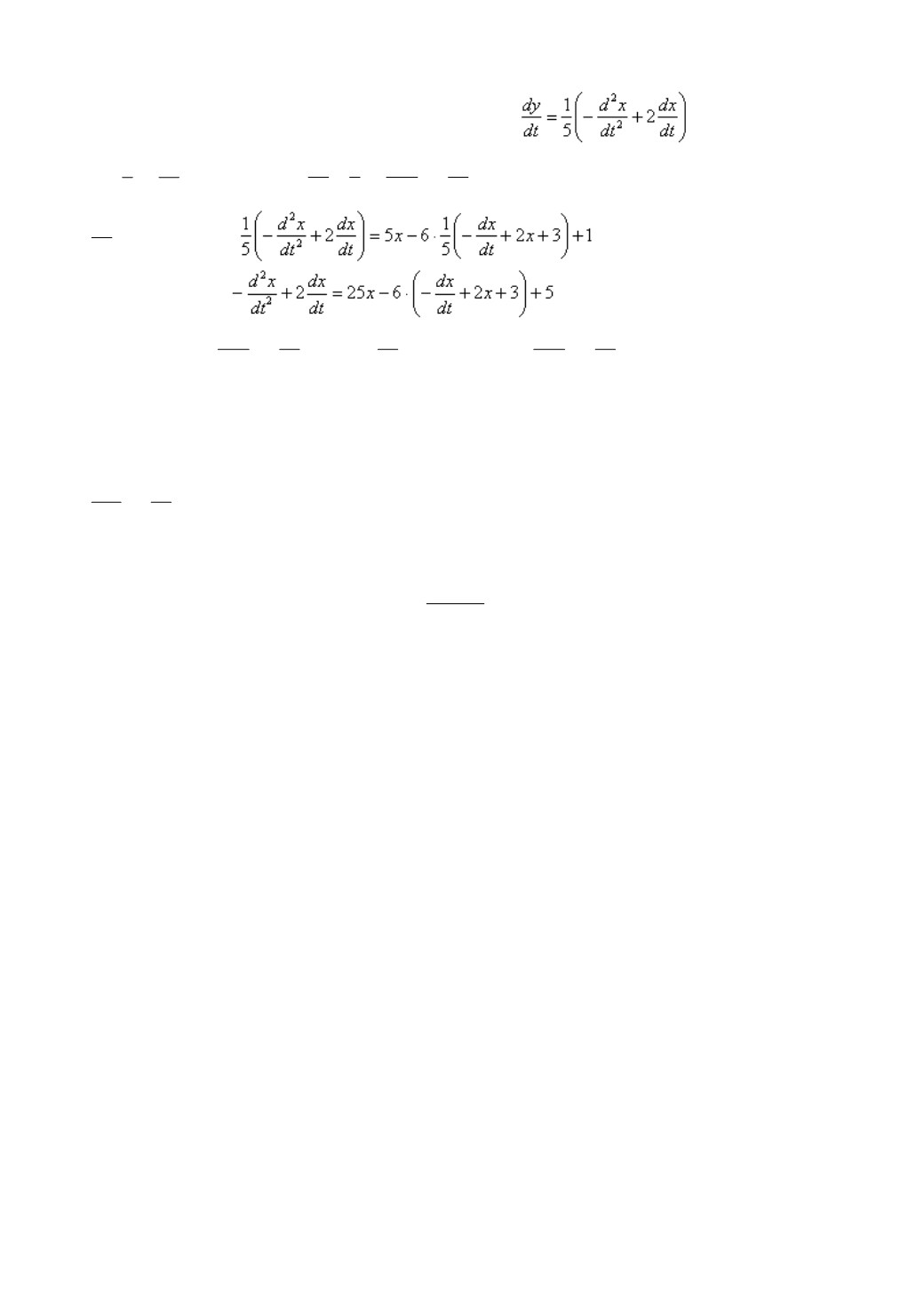
234
Дифференцируем по
t
обе части:
. Подставим
3 2
5
1
x
dt
dx
y
и
dt
dx
dt
xd
dt
dy
2
5
1
2
2
во второе уравнение системы
1 6 5
y x
dt
dy
:
.
Преобразуем:
.
Упростим:
5 18
12
6
25
2
2
2
x
dt
dx
x
dt
dx
dt
xd
,
13 13
4
2
2
x
dt
dx
dt
xd
.
В результате получено
с постоянными коэффициентами.
Найдем общее решение соответствующего однородного уравнения
0 13
4
2
2
x
dt
dx
dt
xd
.
Составим и решим характеристическое уравнение:
0 13 λ4
λ
2
,
36 52
16
D
,
2
6
4
λ
2,1
i
,
i
3
2 λ
2,1
– получены сопряженные комплексные корни, поэтому
t
Ct
C e X
t
3sin
3cos
2
1
2
.
Частное решение неоднородного уравнения ищем в виде
A x
~
.
Найдем первую и вторую производную:
0 ~
t
x
,
0 ~
tt
x
.
Подставим
x
~
,
t
x
~
,
tt
x
~
в левую часть неоднородного уравнения:
13 13
0
4
0
A
,
13 13
A
,
A
=1
.
Таким образом
1
~
x
. В результате
1 3sin
3cos
~
2
1
2
t
Ct
C e x X tx
t
.
Ищем функцию
y
(
t
)
. Сначала находим производную от уже
найденной функции
x
(
t
)
:
.3 sin 2 3 3 cos
3 2
2
3 cos
3 3 sin 3 3 sin
3 cos 2
2
3 cos
3 3 sin
3 sin
3 cos
2
0 3 sin
3 cos
3 sin
3 cos
1 3 sin
3 cos
2
1
2
1
2
2
1
2
1
2
2
1
2
2
1
2
2
1
2
2
1
2
2
1
2
t
С C t
C C e
t
C t
C t
C t
C e
t
C t
C e t
C t
C e
t
C t
C e t
C t
C e
t
C t
C e tx
t
t
t
t
t
t
t t
t
t
t
Подставим в уравнение (8.1)
1
3
sin
3
2
1
2
t
Ct os
C e
t
x
t
и
t
С C
t
C C e
t
x
t
t
3sin
2 3
3cos
3 2
2
2
1
2
1
2
: