228
В нашем случае нам на каждом последующем шаге нужно
одновременно решать оба уравнения и для
y
, и для
z
, т.е. надо решать
четыре уравнения при каждом
x
:
.
Но из преобразований следует, что решение на каждом шаге можно
свести к решению двух уравнений:
,
.
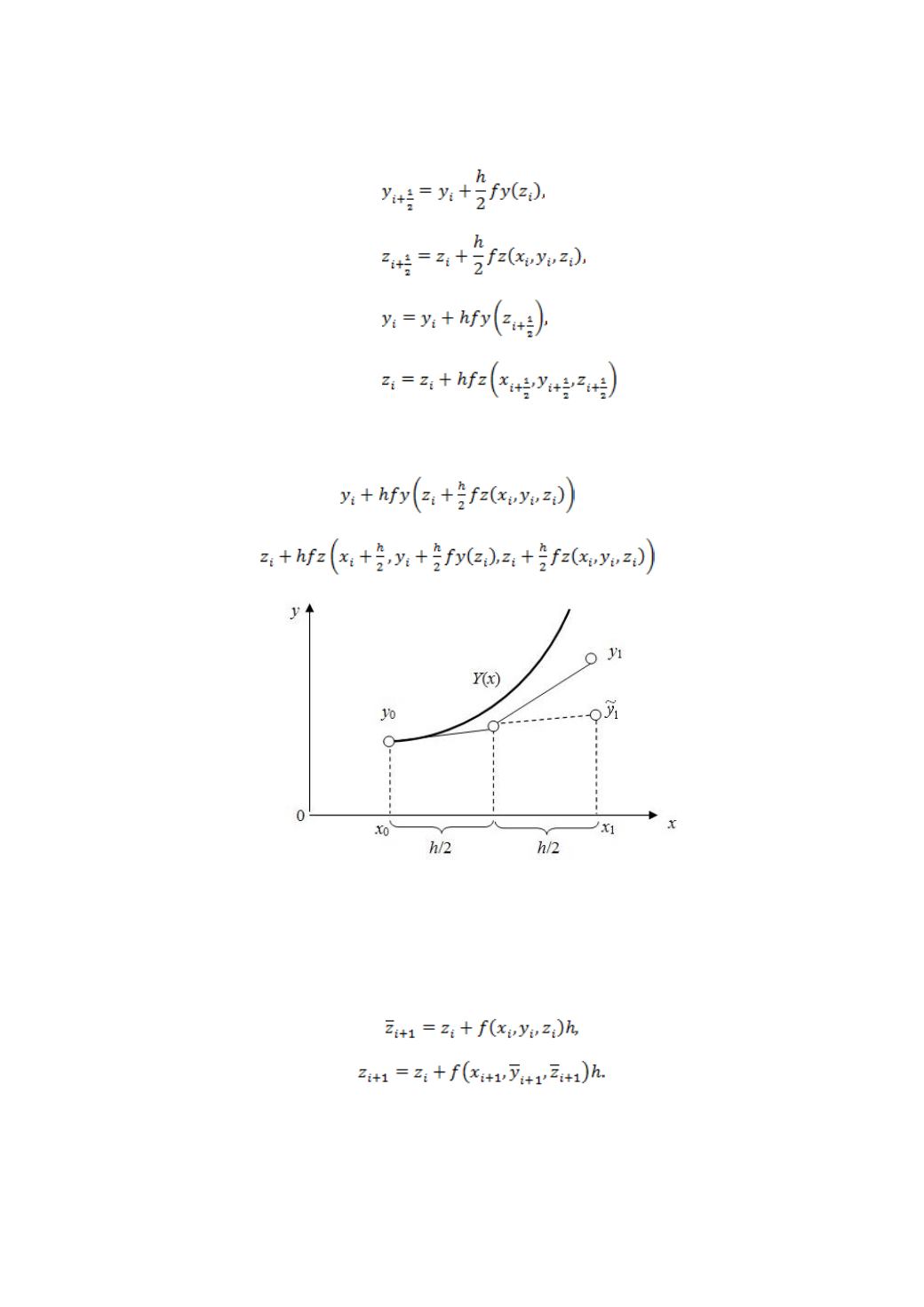
Рис. 8.2. Первая модификация метода Эйлера
Метод Эйлера (вторая модификация)
Вторая модификация метода Эйлера в общем виде делится на два
этапа:
Графически модификация сведена к нахождению биссектрисы угла
между касательной к точке
x
i
и хордой
x
i
- x
i
+1
(рис. 8.3).


