230
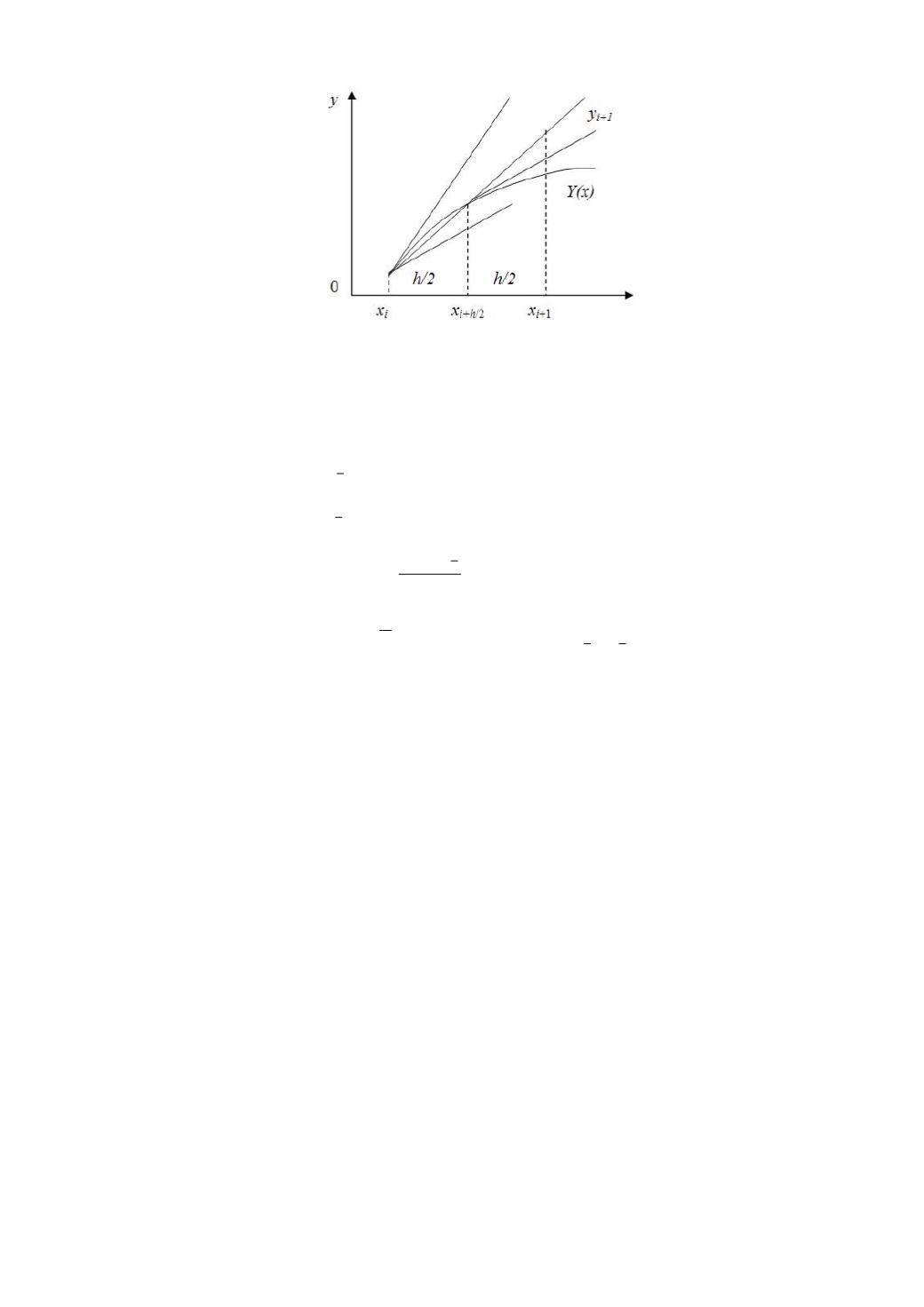
Рис. 8.4. Графическая иллюстрация третьей модификации метода Эйлера
В нашем случае на каждом последующем шаге нужно одновременно
решать оба уравнения и для
y
, и для
z
, т.е. надо решать четыре уравнения
при каждом
x
:
.
,
,
, ,
2
,
2
, ,
,
,
2
1
2
1
1
2
1
2
1
2
1
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
z y x f
zyxf
h
z z
z z
h y y
zyxfh
z
z
z
h y y
Метод Рунге-Кутта
Метод позволяет решать системы обыкновенных дифференциальных
уравнений (ОДУ) первого порядка следующего вида:
,...),
, ,
(
,...),
, ,(
x
y
t
f
x
xy
tg y
которые имеют решение
y=y
(
t
),
x=x
(
t
), где
t
– независимая переменная;
х,
y
и т.д. – искомые функции (зависимые от
t
переменные). Функции
f, g
и
т.д. – заданы. Также предполагаются заданными и начальные условия, т.е.
значения искомых функций в начальный момент.
Одно дифференциальное уравнение – частный случай системы с
одним элементом. Поэтому далее речь пойдет для определенности о
системе уравнений.
Метод может быть полезен и для решения дифференциальных
уравнений высшего (второго и т.д.) порядка, так как они могут быть
представлены системой дифференциальных уравнений первого порядка.


