226
8.3. Линейные неоднородные системы
дифференциальных уравнений
Неоднородная система дифференциальных уравнений, которая в
большинстве случаев может встретиться вам в задачах, имеет следующий
вид:
По сравнению с однородной системой в каждом уравнении
дополнительно добавляется некоторая функция, зависящая от
t
. Функции
f
(
t
) и
g
(
t
) могут быть константами (причем, по крайне мере, одна из них не
равна нулю), экспонентами, синусами, косинусами и т.д.
8.4. Численные методы решения систем
дифференциальных уравнений
Метод Эйлера (простой)
Простейшим и исторически первым численным методом решения
задачи Коши является метод Эйлера. Пусть на отрезке [
a
,
b
] имеем задачу
Коши:
.
) (
),
,( '
0
0
y xy
yxf y
Метод основывается на том, что дифференциальное уравнение может
быть решено на основе представления искомой функции в ряд Тейлора
(причем из разложения в ряд Тейлора берется только первая
производная). Тогда решение представимо в виде
)
)( ('
) (
0
0
0
x x x f
xf y
.
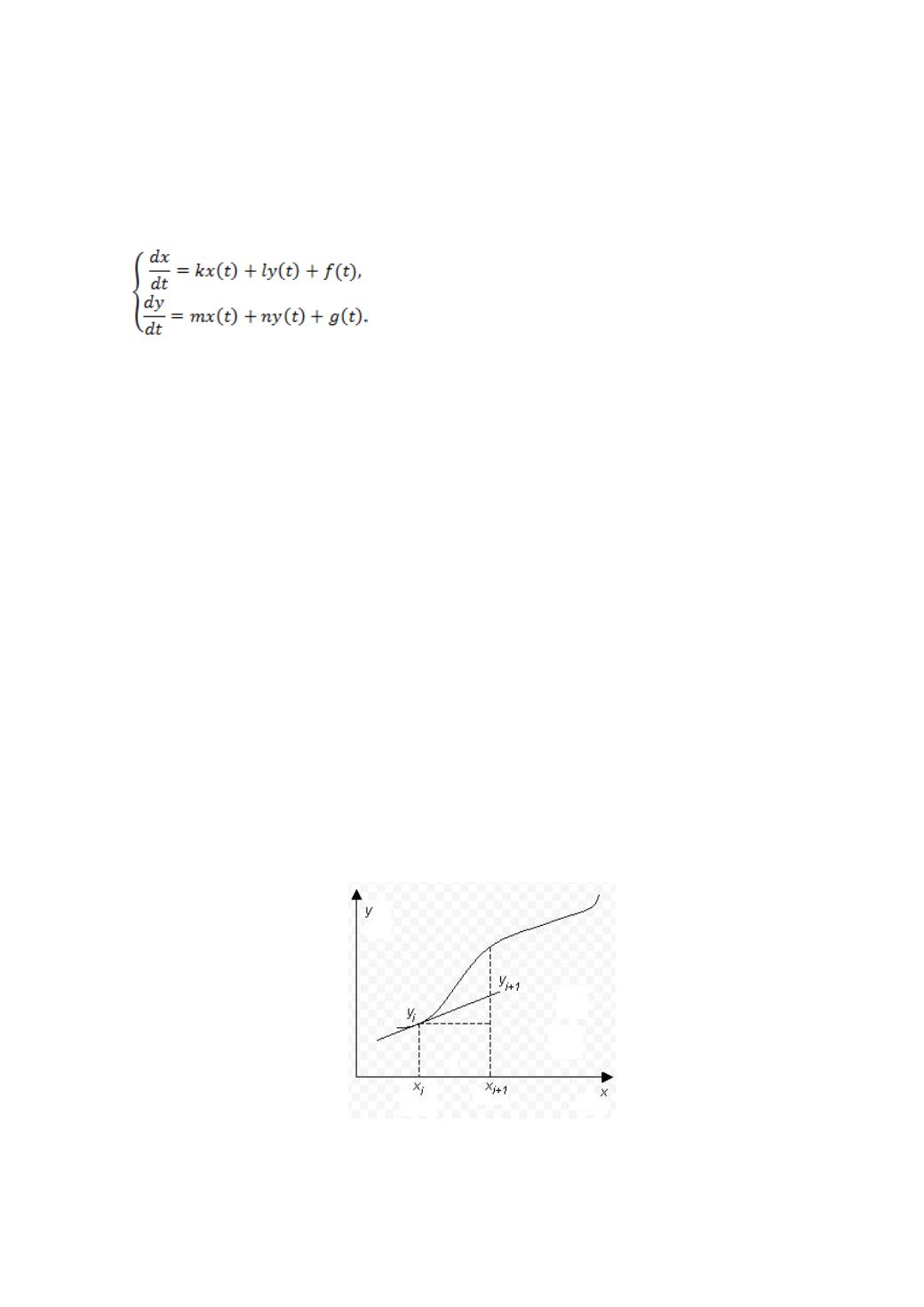
Рис. 8.1. Геометрическая интерпретация одного шага метода Эйлера


