Численные методы решения прикладных задач - page 219

219
Уравнение (7.41) является линейным дифференциальным
уравнением. Найдем решение соответствующего ему однородного
уравнения. Имеем
  pb nk
dt
dp
  ;  dt b nk
p
dp
 ;
  C t bnk p ln ln   ;
   t bn
Ce tp
 ln . (7.42)
В качестве частного решения уравнения (7.41) можно использовать
стационарное равновесное решение   const   p tp , где p  корень
уравнения    ps p d  (в этом случае обе части уравнения (7.39) будут
равны нулю). Из (7.41) нетрудно найти, что (рис. 7.10)
nb
m a
p


 .
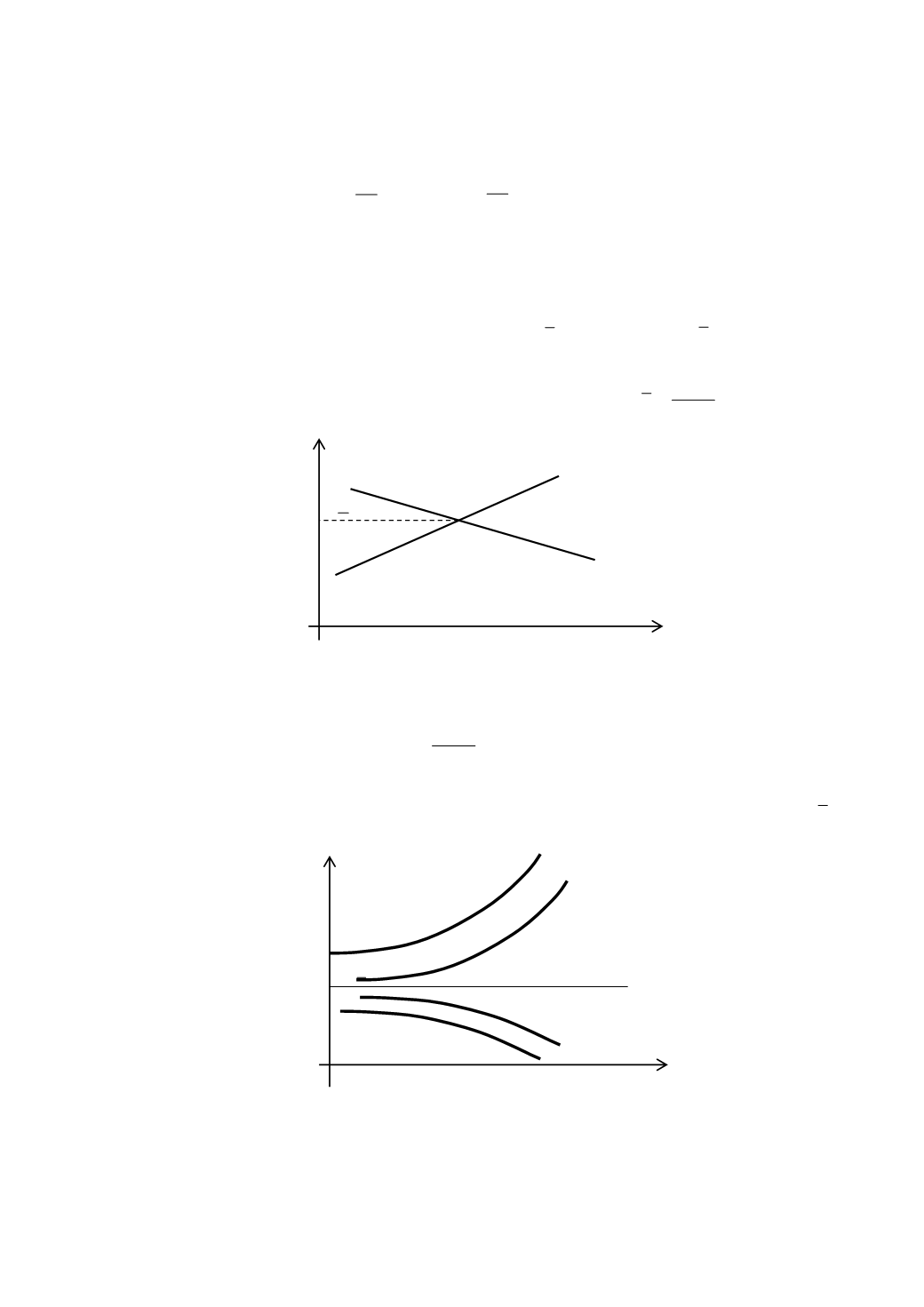
Рис. 7.10. Стационарное равновесное решение
Таким образом, общее решение уравнения (7.41) имеет вид
   tbnk
Ce
nb
ma
t p 



 . (7.43)
Из (7.43), в частности, вытекает, что если n >b , то с течением времени
интегральные кривые будут отдаляться от состояния равновесия p
(рис. 7.11).
Рис. 7.11. Интегральные кривые отдаляются от состояния равновесия
Если n = b , то p (t) = const (рис. 7.12).
s
(p)
d
(p)
p
p
q
t
p
p