218
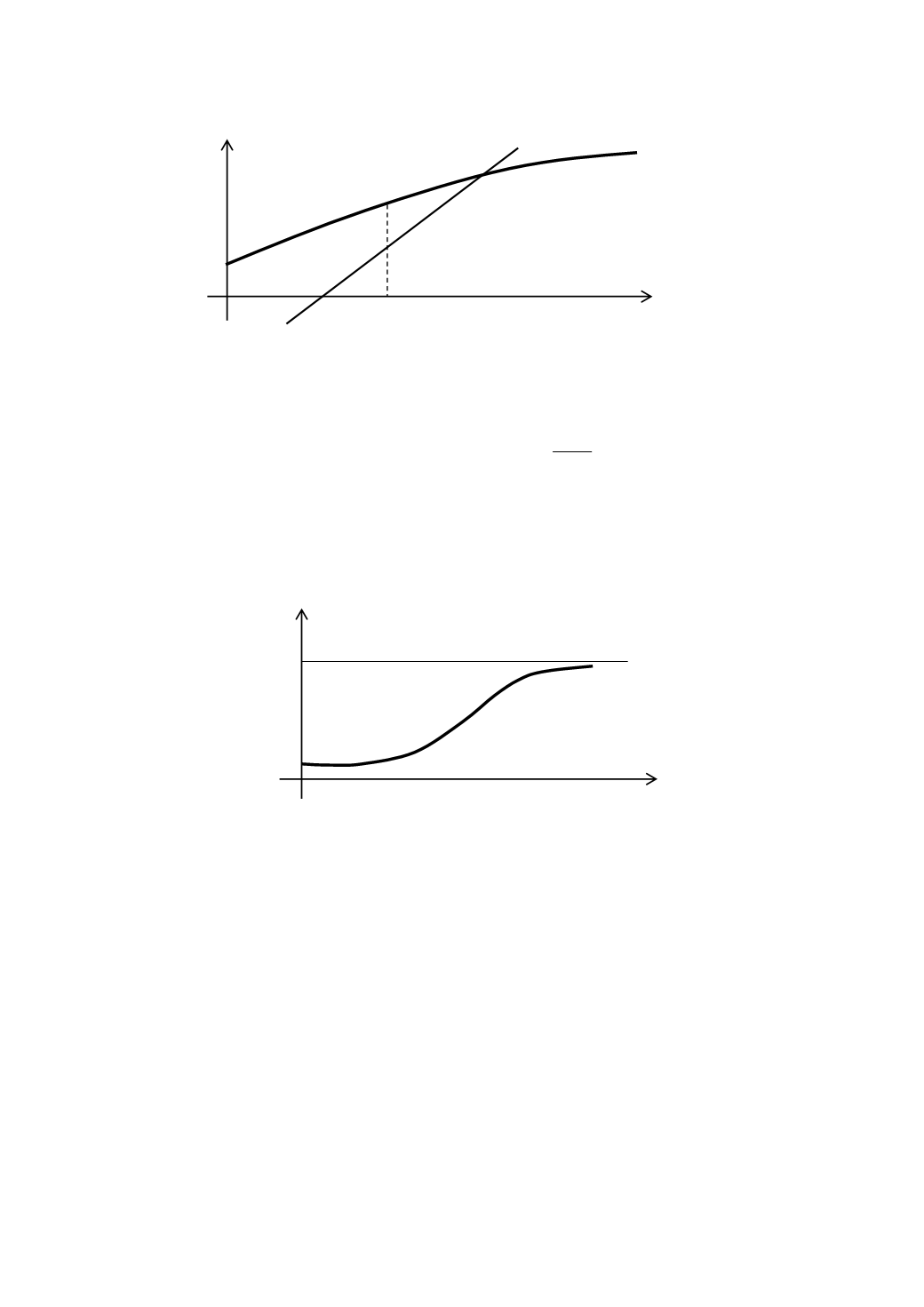
Рис. 7.8. Графический вид уравнения неоклассического роста
Кроме того, так как
k f
непрерывная монотонно убывающая
функция, то существует такое
l
k
, что
l
k f
l
β
α
(т.е. у
tk
существует
точка перегиба). Итак, при
*
k
k
имеем
0
k
; при
*
k k
будет
0
k
. При
l
k k
имеем
0
k
, а при
l
k k
,
0
k
.
Ввиду этого интегральная кривая уравнения (7.38) очень
напоминает логистическую кривую (рис. 7.9).
Рис. 7.9. Логистическая кривая
Пример 7.9
Рассмотрим уравнение Самуэльсона
pS p
dk p
.
(7.39)
Моделирующее
связь
между
изменением
цены
p
и
неудовлетворенным спросом
p
s
pd
(здесь
p
d
и
p
s
соответственно
величины спроса и предложения при цене
p
,
0
k
). Предположим, что
спрос и предложения задаются линейными функциями
bp a pd
,
np
m
p
s
,
(7.40)
где
a
,
b
,
m
,
n
– некоторые положительные числа. С учетом (7.40)
уравнение (7.39) примет вид
m
akp
pnk
p
.
(7.41)
k
*
k
t
k
k
*
0
y=lf
(
k
)
y=
(
+
)
k


