211
процессов выхода к состоянию равновесия, так и процессов
трансформации самого этого состояния под воздействием внешних сил.
Рассмотрим простую экономическую систему в состоянии
равновесия и опишем движение такой системы в непрерывном времени.
Дифференциальное уравнение связывает изменение показателя (пусть
наша система описывается одним показателем
x
(
t
)
) со скоростью
движения
t
x
. Будем считать, что скорость изменения показателя
пропорциональна величине его отклонения от равновесного значения
e
x
.
Чем дальше показатель отклонился от равновесного значения, тем
быстрее он стремится вернуться к нему. Если в уравнении присутствует
только первая производная
х
по времени, а сама связь линейна, то это
линейное дифференциальное уравнение. Пусть оно имеет, например,
следующий вид:
e
x
xk x
,
где
k
- коэффициент.
Частное решение
e
x
x
, общее решение
kt
e
ce x x
. При
t
=0 получаем
e
x x
c
0
,
kt
e
e
e
x
x
x
t
x
0
. Если
k
<0
, то
0
kt
e
- равновесие устойчиво,
т.е. при отклонении
x
(
t
) от значения
х
е
она вновь стремится принять это
значение. При
k
>0
e
kt
→∞ и соответственно
x
(
t
)→
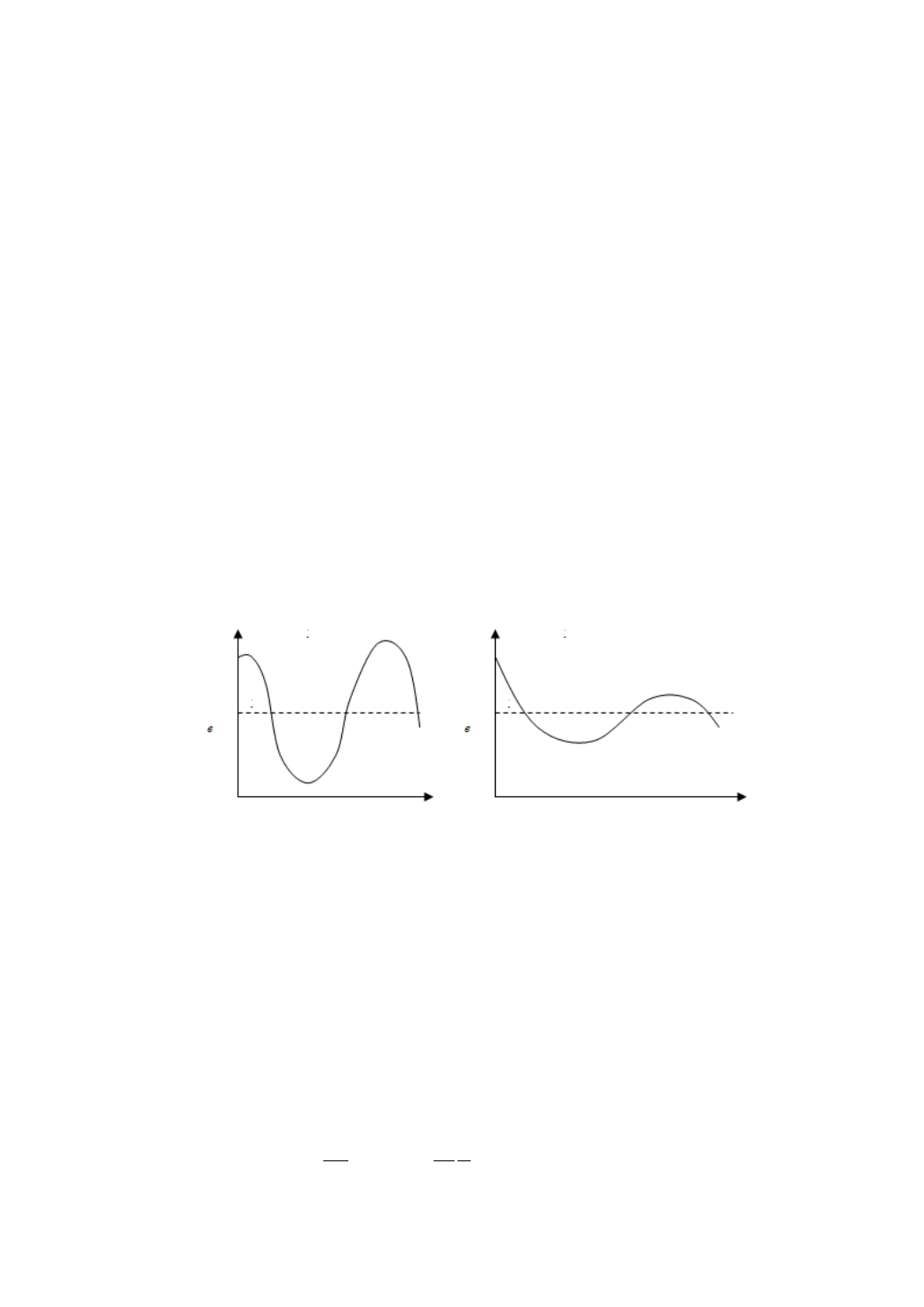
(рис. 7.1).
Рис. 7.1. Поведение динамических систем
Рассмотрим модель рынка с прогнозируемыми ценами. В простых
моделях рынка обычно полагают, что спрос и предложение зависят
только от текущей цены на товар. Однако в реальных ситуациях они
зависят еще и от тенденции ценообразования, и от темпов изменения
цены. В моделях с непрерывными и дифференцируемыми по времени
t
функциями эти характеристики описываются соответственно первой и
второй производной функции цены
P
(
t
).
Пример 7
.5
Математические модели экономического роста
(уравнения с разделяющимися переменными)
Найти функцию, имеющую постоянную эластичность равную
k
. По
условию задачи имеем
k
y
xy
, т.е.
k
y
x
dx
dy
.
t


