Численные методы решения прикладных задач - page 215

215
 
kdt
ay by
dy


, или kdt
ay b
a
y b
dy








1 .
Проинтегрировав это соотношение, имеем C kbt ay b yln ln ln    ,
т.е. kbt Ce
ay b
y


.
Отсюда получим, что
kbt
kbt
Ce
Cbe
y


1
. (7.34)
График функции (7.32) называется логистической кривой. Она также
описывает некоторые модели распространения информации (рекламы),
динамику эпидемий и др.
Замечание. Из графика логистической кривой видно, что при малых t
логистический рост схож с естественным ростом, однако при больших t
характер роста меняется, темпы роста замедляются, и кривая
асимптотически приближается к прямой
a
b
y  . Эта прямая является
стационарным решением уравнения (7.33) и соответствует случаю
  0  y p . Для уравнения (7.33) также существуют решения и при
a
b
y  ,
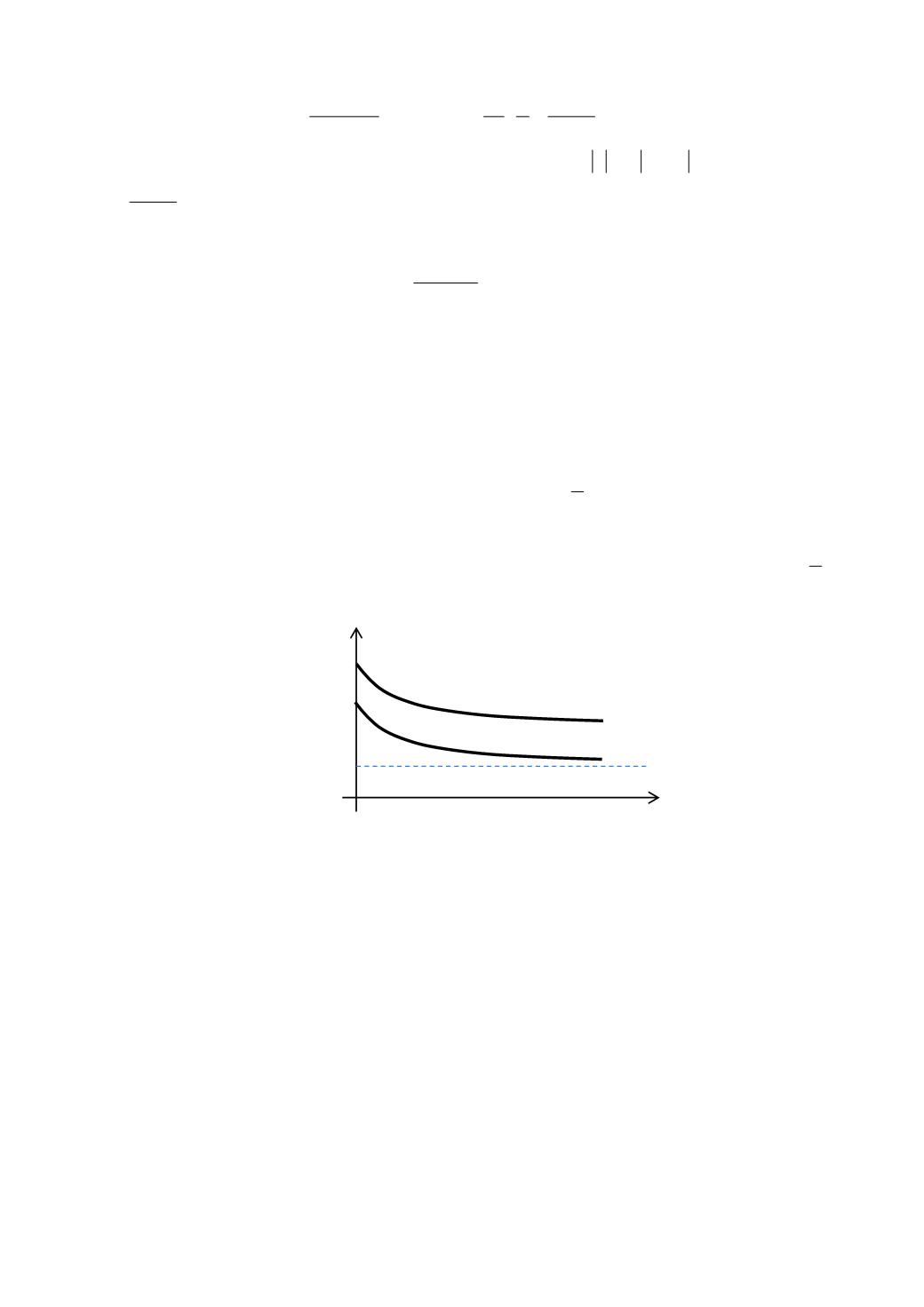
имеющие графики (рис. 7.4).
Рис. 7.4. Логистическая кривая
Но, так как в этом случае   0  yp , то эти графики не имеют
экономической интерпретации.
Замечание. Более реалистичной является модель, в которой
скорость роста зависит не от дохода, а от прибыли. Пусть   β α   y y C 
издержки (,   константы) тогда
   
β α    y yyp k y . (7.35)
Если   ay b yp  , то правая часть уравнения (7.35) представляет
собой квадратный многочлен относительно y с отрицательным
коэффициентом перед 2
y . В этом случае возможны три варианта.
t
y
b
/a
0