214
Рассмотрим более общий случай по сравнению с предыдущим
пунктом. Пусть
y
p p
– убывающая функция
0
dy
dp
, т.е. увеличением
выпуска будет происходить насыщение рынка, и цена будет падать.
Проведя аналогичные рассуждения, получим уравнение
yy
kp y
,
(7.31)
здесь
k
=
l
. Уравнение (7.31) представляет собой автономное
дифференциальное уравнение. Так как
0
k
,
0
p
,
0
y
, то из (7.31)
следует, что
ty
есть возрастающая функция (
0
y
). Исследуем
t
y
на
выпуклость. Дифференцируя уравнение (7.31) по
t
, получим
p y
dy
dp
yk y
или
1
p
y
dy
dp
pyk y
, т.е.
y
e
pyk
y
1
1
,
(7.32)
где
p
y
dy
dp
pe
y
эластичность спроса.
Из (7.32) вытекает, что если спрос эластичен, т.е.
1
y
e
, то
0
y
,
(функция спроса – выпуклая функция), а если спрос неэластичен, т.е.
1
y
e
, то
0
y
(функция спроса – вогнутая функция).
Пусть, например,
ay b yp
(
a
,
b
> 0), тогда уравнение (7.32)
принимает вид
y
ay
b
k y
.
(7.33)
Из (7.33) легко получить, что
0
y
, если
0
y
, или
a
b
y
, а также,
что
0
y
при
a
b
y
2
, и
0
y
при
a
b
y
2
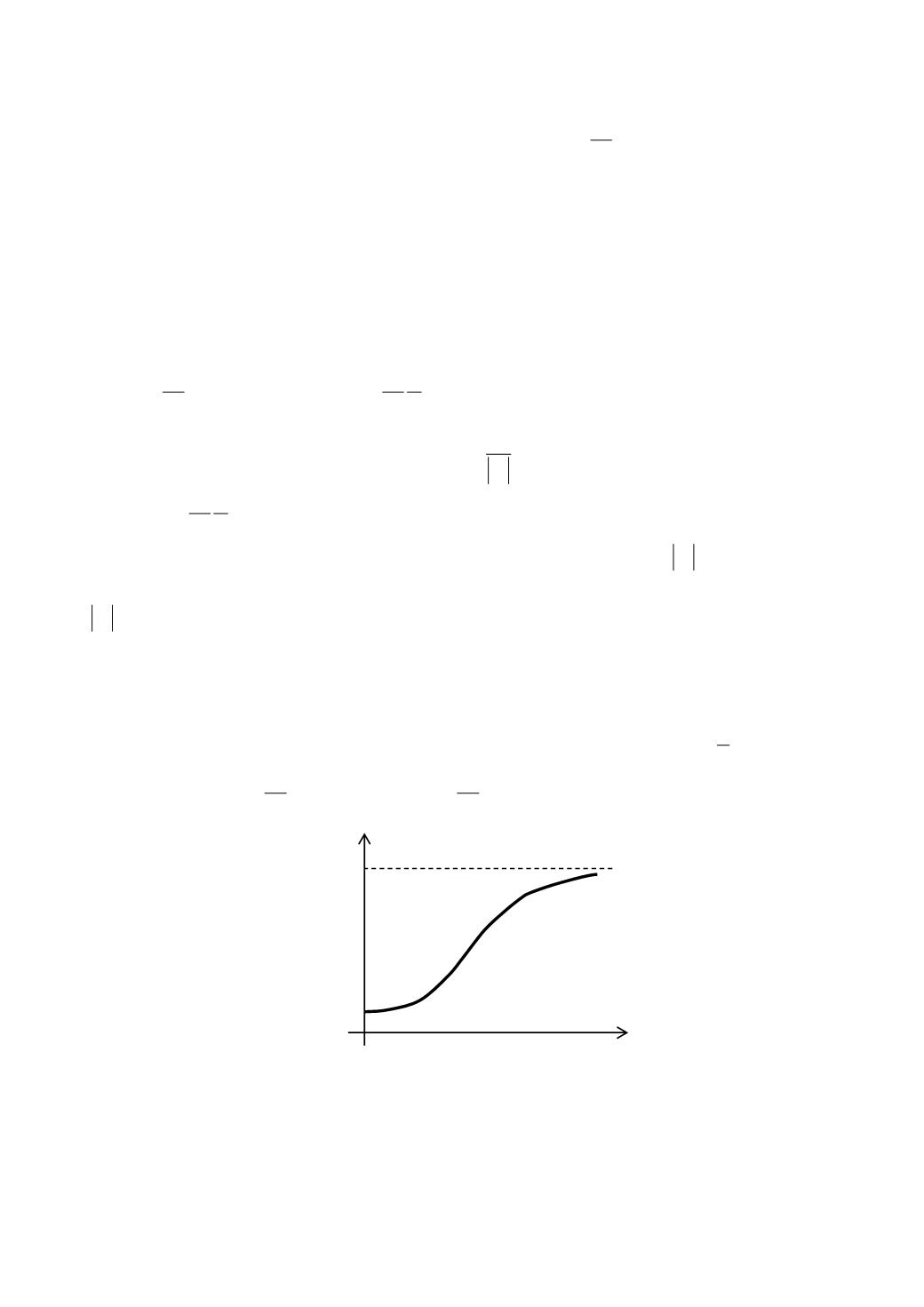
(рис. 7.3).
Рис. 7.3. Функция спроса
В данном случае довольно легко получить явное выражение для
ty
.
Разделяя переменные в уравнении (7.33), находим
t
0
y
b
/a


