32
что из набора
N
ценных бумаг можно сформировать бесконечное число порт-
фелей. Теорема об
эффективном множестве
гласит: инвестор выберет свой
оптимальный портфель из множества портфелей, каждый из которых обеспе-
чивает: максимальную ожидаемую доходность для некоторого уровня риска и
минимальный риск для некоторого значения ожидаемой доходности. Набор
портфелей, удовлетворяющих этим двум условиям, называется эффективным
множеством.
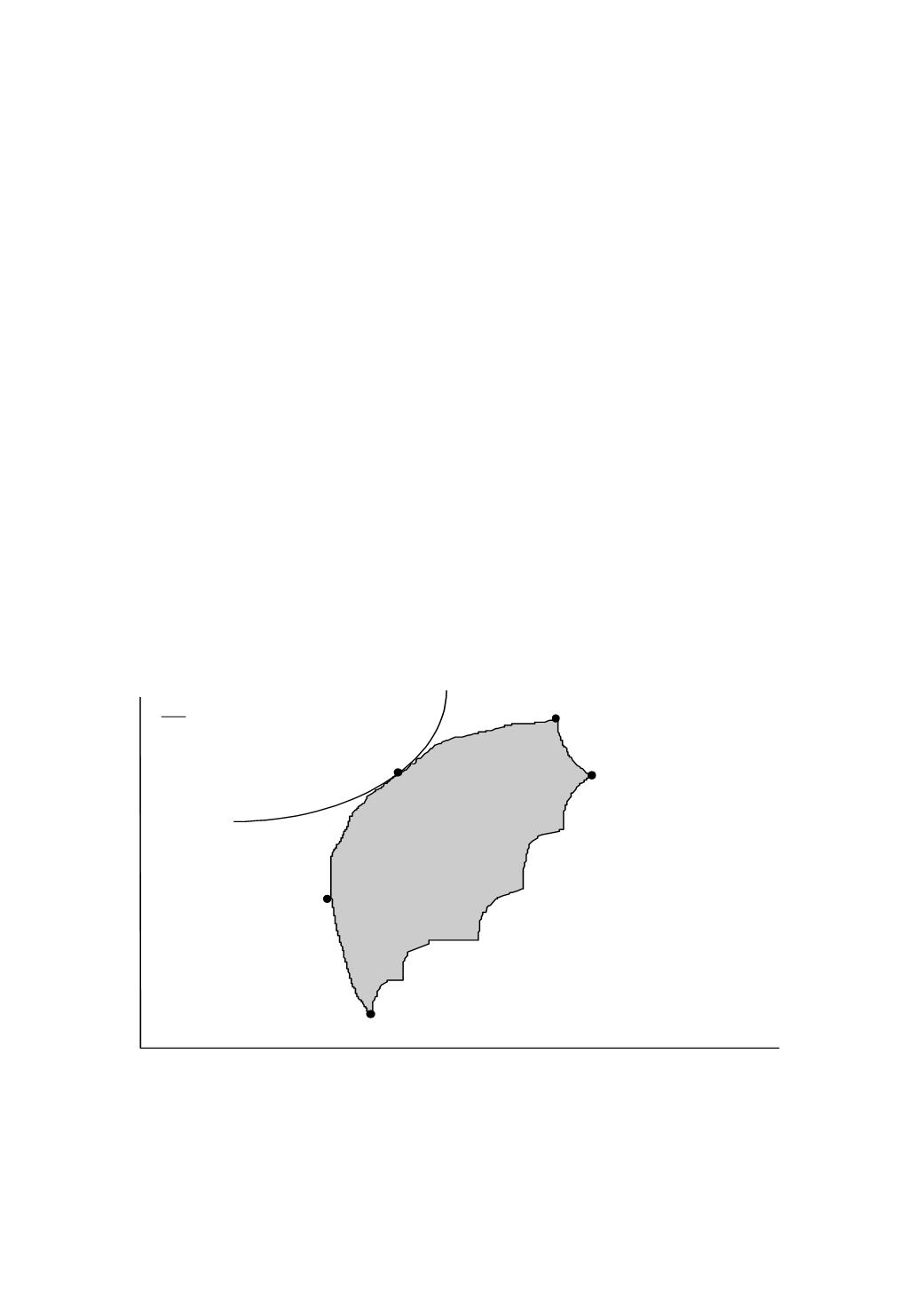
На рис. 2.2 представлена иллюстрация достижимого множества, представляю-
щего собой все портфели, которые могут быть сформированы из группы в
N
ценных бумаг (точки
G
,
E
,
S
и
H
являются примерами таких портфелей). Точка
S
– соответствует наибольшей ожидаемой доходности,
G
– наименьшей,
Е
–
минимальному риску,
Н
– максимальному риску. Эффективное множество
портфелей лежит на верхней и левой границы достижимого множества между
точками
Е
и
S
. Все остальные достижимые портфели являются неэффективны-
ми. Инвестор должен нарисовать свои кривые безразличия на одном рисунке с
эффективным множеством, а затем приступить к выбору портфеля, располо-
женного на кривой безразличия, находящейся выше и левее остальных. Опти-
мальной точкой является точка касания
О
кривой безразличия инвестора с кри-
вой множества эффективных портфелей.
Рис. 2.2. Выбор оптимального портфеля
Ранее было отмечено, что существует бесконечное число портфелей, до-
ступных для инвестора. В то же время инвестор должен рассматривать только
те портфели, которые принадлежат к эффективному множеству. Однако это
r
p
p
E
G
O
H
S
Достижимое
множество


