106
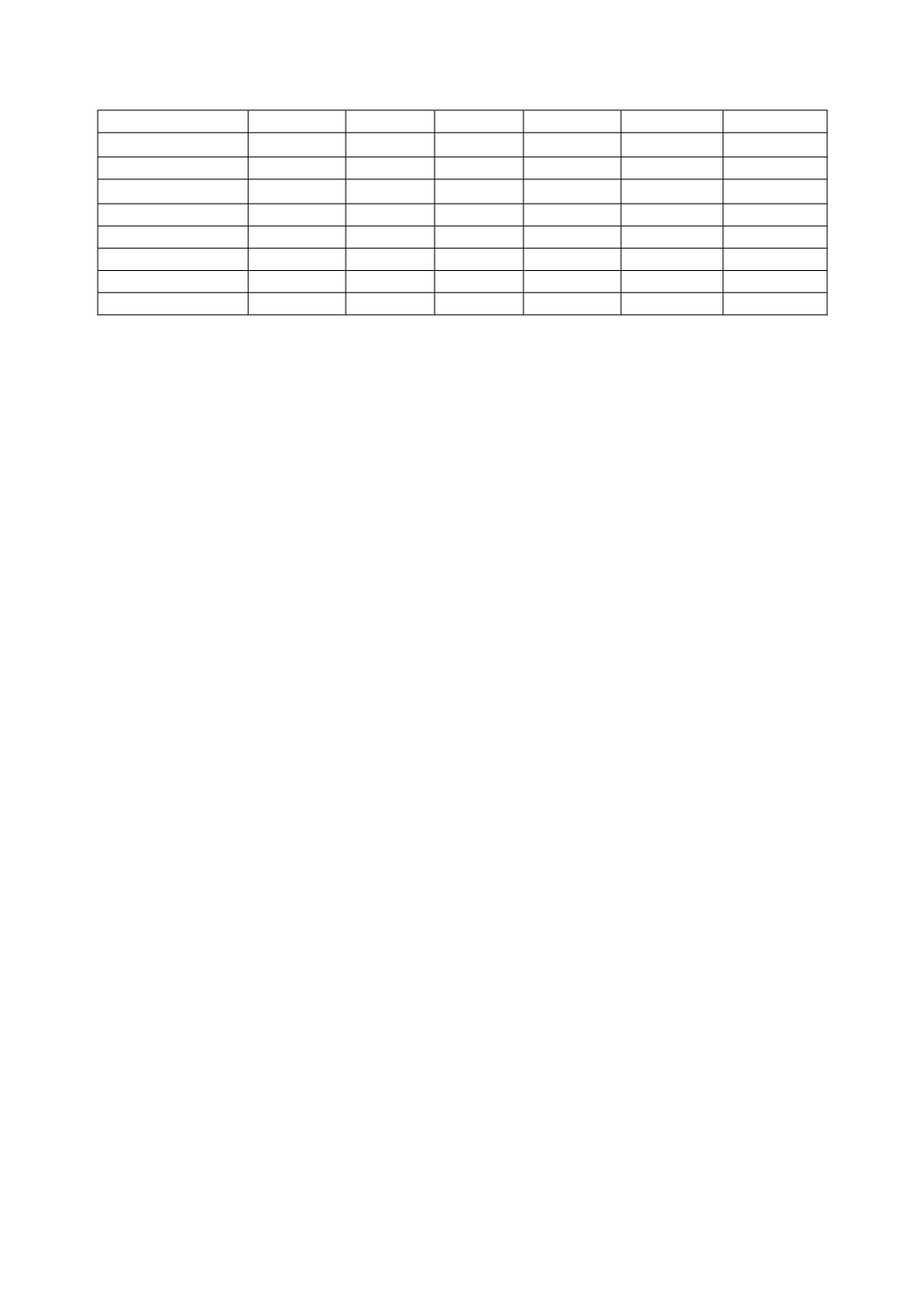
Таблица 1
v
0
, м/с.
0,5
1,0
1,5
2,0
2,5
16
τ
(
v
0
), мксек.
105,69
91,99
84,86
80,07
76,59
52,85
F
(
v
0
), (нъютон)
959,52
2204,28
3586,69
5065,44
6619,73
61409,28
P
z
(0,0), (ГПа)
3,402
4,493
5,278
5,923
6,475
13,606
a
(
v
0
), (мм)
0,367
0,484
0,5696
0,639
0,6987
1,4680
h
0
(
v
0
), (мкм)
17,96
31,27
43,26
54,45
65,08
287,33
a
2
/
h
, (мм)
7,4994
7,4914
7,4998
7,4990
7,5012
7,5002
U
, (мДж)
6,892
27,568
62,058
110,301
172,267
7055,648
T
, (мДж)
13,784
55,135
124,054
220,540
344,594
14114,56
Расчет длительности соударения
( )
0
τ
v
проведен в п. 4.8.
Из приведенных в таблице данных видно, что в рассмотренном диапазоне
относительной скорости
0
v
соударения шаров
( )
( )
0 0
0
h v a v R
.
Значения отношения
a
2
/
h
с большой точностью совпадают с
/ 2 7,5 мм
R
=
,
что свидетельствует о высокой точности полученных для
( )
0
a v
и
( )
0 0
h v
значе-
ний. Суммарная потенциальная энергия упругой деформации столкнувшихся
шаров равняется кинетической энергии налетающего шара.
4.7. Шар и цилиндр на плоскости
Шар на плоскости
. Шар радиуса
R
соприкасается с плоскостью (с уп-
ругим полупространством). Это является частным случаем рассмотренной выше
задачи, когда
R
<<
R
′→ ∞. В этом случае из (4.65) следует, что
Λ
= 1/(2
R
), а из
(4.66) и (4.67) следует, что
a
= (
FDR
)
1/3
.
Следовательно,
h
=
FD
/
a
=(
F
2
D
2
/
R
)
1/3
(4.70)
Как и следовало ожидать,
a
2
/
h
=
R
.
В однородном упругом изотропном полупространстве вокруг точки каса-
ния возникнет деформация, описываемая уравнениями (2.115), и одновременно
возникнет вдавление в первом шаре с центром в точке касания, определяемое
значением радиуса области касания
a
и величиной
h
=
a
2
/
R
.
Вследствие этого шар и плоскость будут соприкасаться некоторой по-
верхностью вращения, радиус главного сечения которой будет больше, чем ра-
диус кривизны недеформированного шара. Вследствие этого при верчении шара
или плоскости вокруг нормали (ось z) в точке касания шара с плоскостью воз-
никнет сила трения верчения (гл. 1). В сущности, процесс трения верчения яв-
ляется разновидностью трения скольжения, когда одновременно присутствуют
разные относительные скорости скольжения различных участков твердых кон-
тактирующих поверхностей при различных значениях давления. В задачах (1.9)
и (1.10) сила трения верчения не учитывается.
Формулы (4.70) могут быть использованы для теоретической оценки сил
трения верчения, измеряемых на эксперименте (см. п. 1.4.3, гл. 1).
Цилиндр на плоскости.
Один из тел является однородным цилиндром, а
второй - упругим полупространством. Это является частным случаем рассмот-


