136
)
)(
(
)
)(
(
)
)(
(
)
)(
(
)
)(
(
)
)(
(
)(
1
2
2
1
2
2
1
1
2
1
2
1
2
1
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
x
x x
x
x x x x
y
x x x
x
x x x x
y
x x x x
x x x x
y xS
.
В результате получим
2
2
2
2
3
4.5 1.5,
0 1,
( )
5 4 ,
1 3,
8 17,
3
5.
x
x
x
S x
x x
x
x x
x
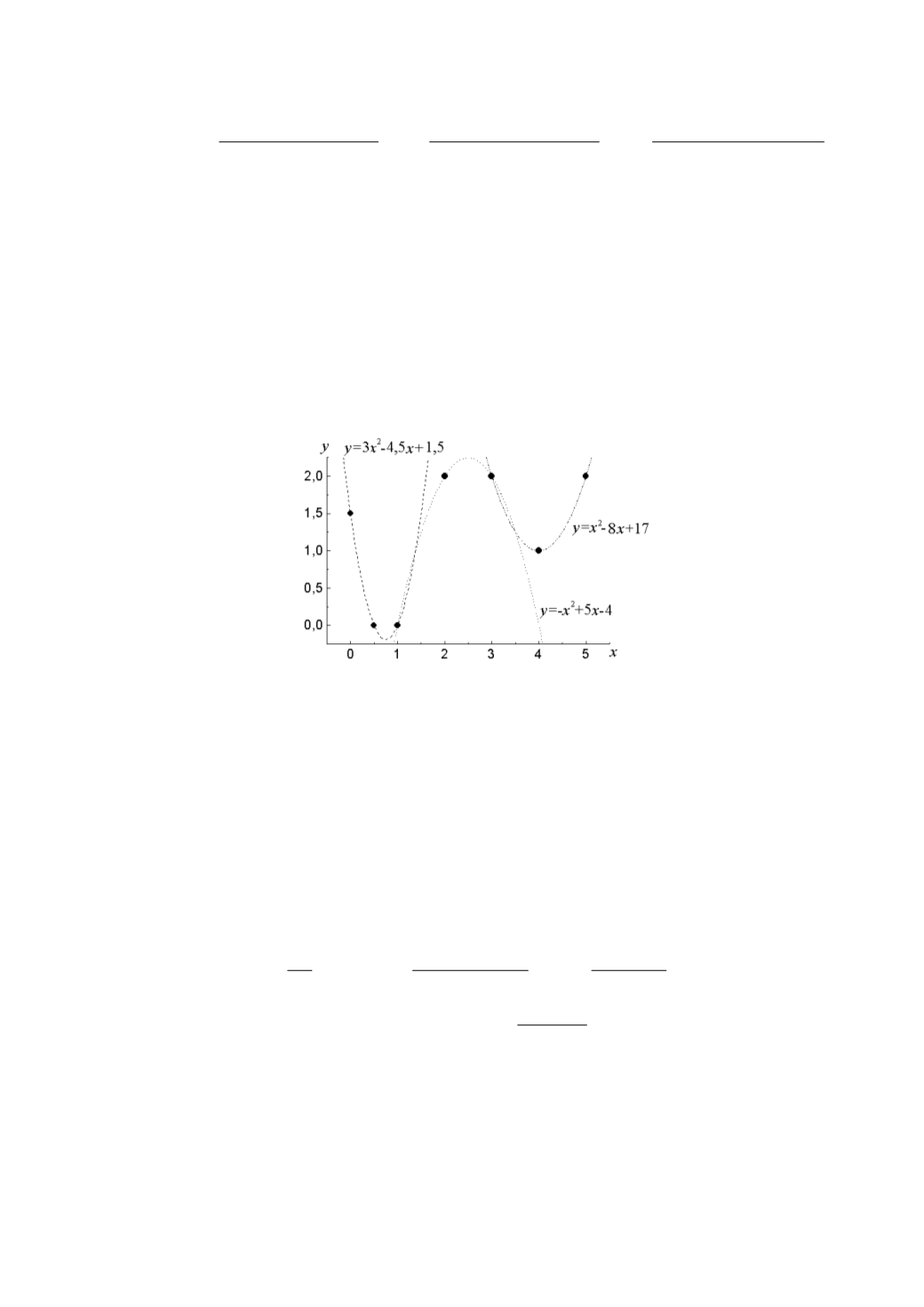
График полученного кусочно-квадратичного интерполирования
представлен на рис. 4.15.
Рис. 4.15. Кусочно-квадратичная интерполяция
Пример 4.9
Найти смыкающийся кубический сплайн, проходящий через точки:
(0;0), (1;0,5), (2;2), (3;1,5). Первая производная удовлетворяет граничным
условиям
2,0
)0
(
'
S
и
1
)3(
'
S
.
Решение. Кубический сплайн состоит из кубических полиномов
3
3,
2
2,
1,
0,
)
(
)
(
)
(
)(
)(
k
k
k
k
k
k
k
k
x x s
x x s xx s s x
S
xS
,
где
1
0
N
k
,
N
количество точек (
х
к
, у
к
), а
1
k
k
x
x x
.
Коэффициенты сплайна
)(
xS
вычисляются по формулам:
k
k
y
s
0
,
,
2
1,
k
k
m
s
,
6
)
2(
1
2,
k
k
k
k
k
mm h
d s
,
k
k
k
k
h
m m
s
6
1
3,
,
(4.51)
где
) (
"
k
k
x
S m
;
) (
"
1
1
k
k
x
S m
;
k
k
k
x x h
1
;
k
k
k
k
h
y y
d
1
.
Для вычисления
k
m
применяется следующая формула:
k
k k
k k
k
k
k
u mh mh h
mh
1
1
1 1
)
(2
,
(4.52)
где
)
(6
1
k
k
k
d d
u
для
2 ,...2,1
N k
.


