139
Из системы (4.55) получим уравнения:
.
12
4
,6
4
3
2
1
2
1
0
m m m
mm
m
Подставляя
0
m
и
3
m
в систему (4.55) получим:
.
12
4
,6
4
2
1
2
1
m
m
mm
Решая эту систему, получим, что
4
,2
1
m
и
6,3
2
m
Значения
0
0
m
,
4,2
1
m
,
6,3
2
m
,
0
3
m
подставляем в (4.54) и
находим коэффициенты сплайана.
Решением является:
2 )2 (
7,0 )2 (8,1
)2 (6,0
)(
5,0 )1 (3,1
)1 (2,1 )1
(1 )(
1,0 4,0
)(
2
3
2
2
3
1
3
0
x
x
x
xS
x
x
x
xS
x
x
x
S
для
.3 2
,2 1
,1 0
x
x
x
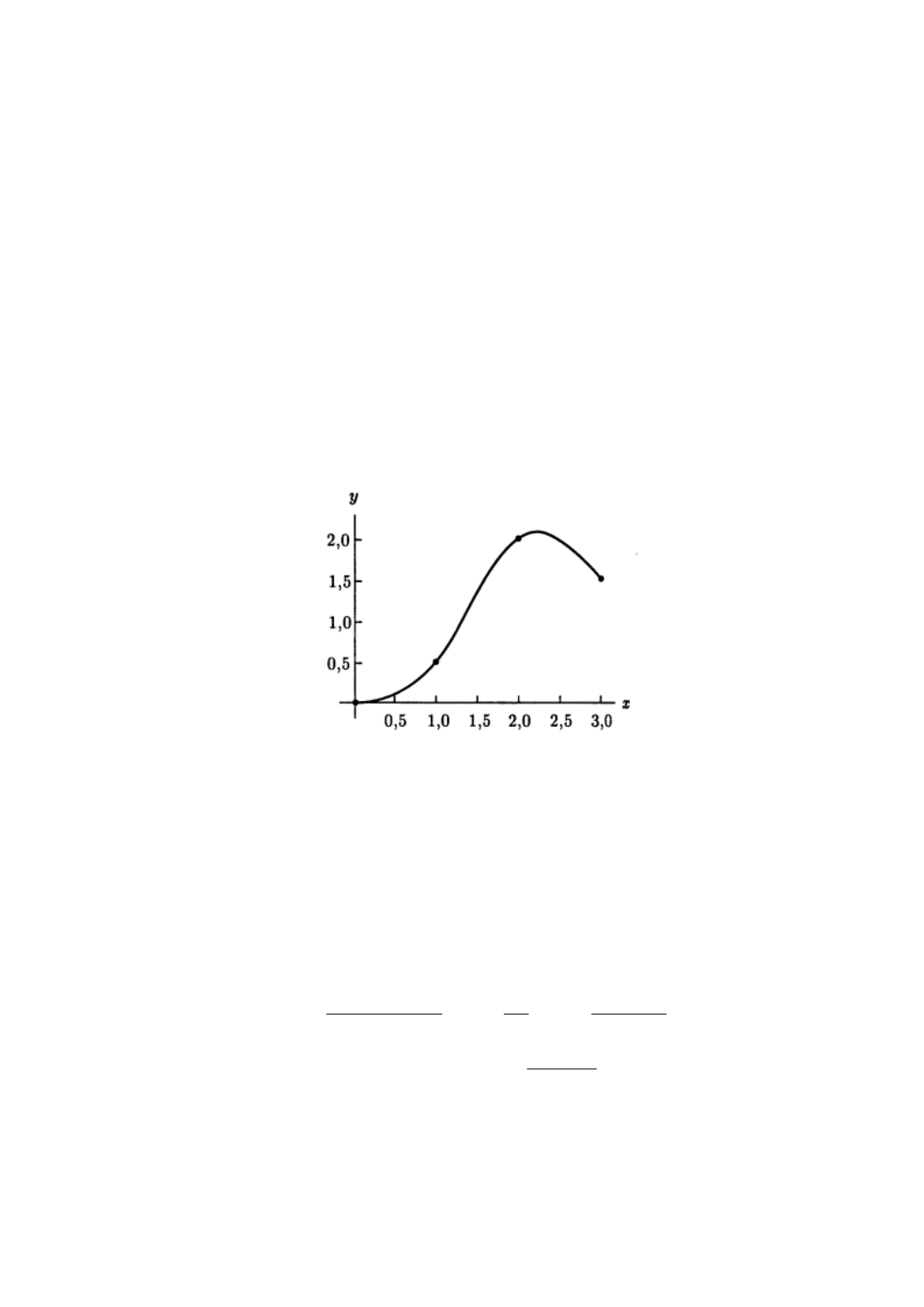
Естественный кубический сплайан показан на рис. 4.17.
Рис. 4.17 Естественный кубический сплайн
Пример 4.11
Найти экстраполяционный кубический сплайн, проходящий через
точки: (0;0), (1;0,5), (2;2), (3;1,5).
Решение. Кубический сплайн состоит из кубических полиномов
3
3,
2
2,
1,
0,
)
(
)
(
)
(
)(
)
(
k
k
k
k
k
k
k
k
x x s
x x
s
xx
s s
x
S x
S
,
где
1
0
N
k
,
N
количество точек
(х
к
, у
к
)
, а
1
k
k
x
x x
.
Коэффициенты сплайна
)(
xS
вычисляются по формулам:
k
k
y
s
0
,
,
6
)
2(
1
2,
k
k
k
k
k
mm h
d
s
,
2
1,
k
k
m
s
,
k
k
k
k
h
m m
s
6
1
3,
(4.57)
где
) (
"
k
k
x
S m
,
)
("
1
1
k
k
x
S
m
,
k
k
k
x x h
1
,
k
k
k
k
h
y y
d
1
.
Для вычисления
k
m
применяется следующая формула
k
k k
k k
k
k
k
u mh mh h
mh
1
1
1 1
)
(2
,
(4.58)


