133
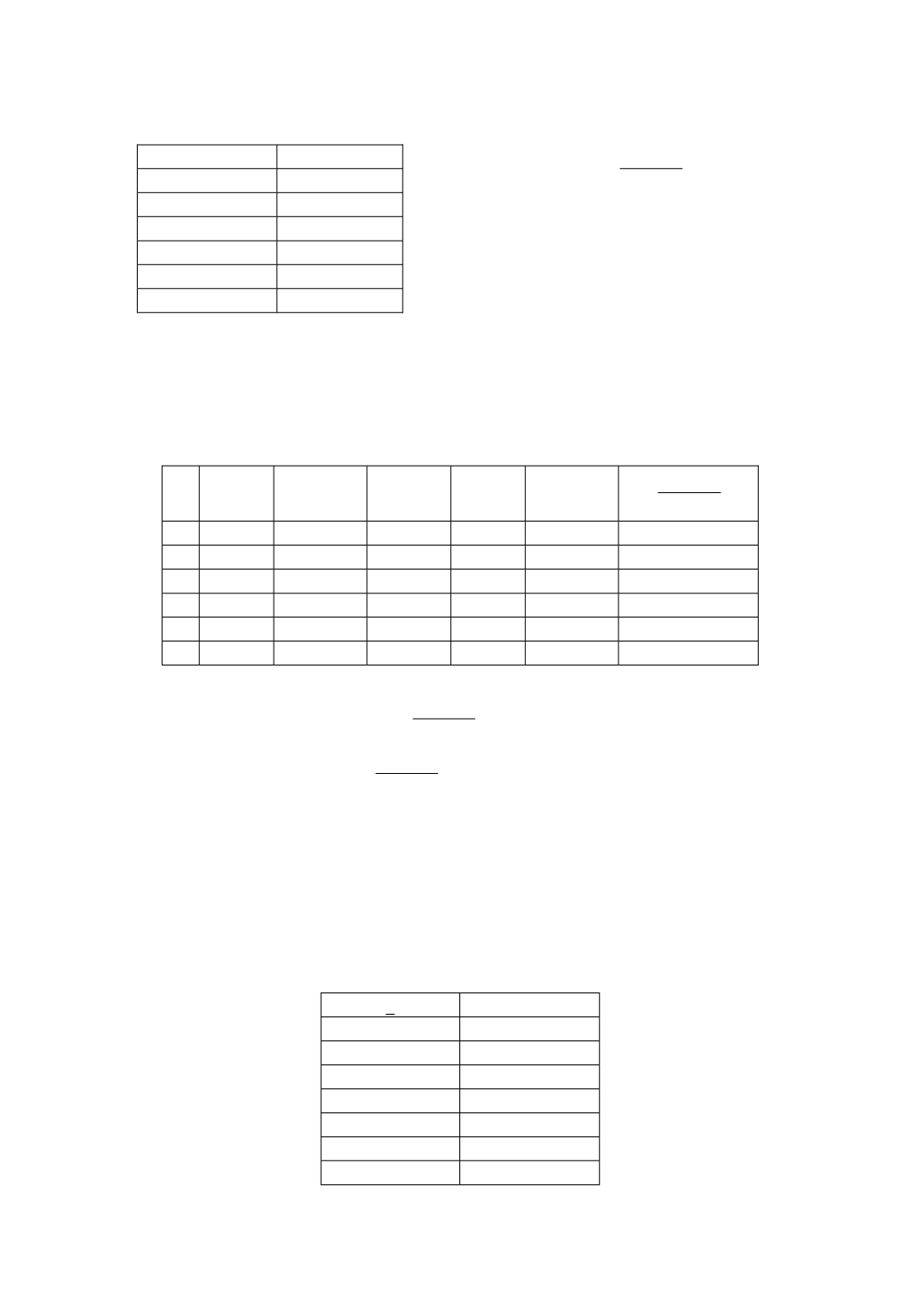
Таблица 4.10
Исходные данные
х
у
0,101
1,26183
0,106
1,27644
0,111
1,29122
0,116
1,30617
0,121
1,32130
0,126
1,32660
Решение.
Вычисления
производим
по
формуле
1
0
) (
)
(
)
(
n
n
i
i
i
C
i t
y
t
xf
,
где
)
)...( 2
)(1 ( )(
1
n t
t
tt t
n
,
h x
x t
/
)
(
0
,
i
i
x x
h
1
,
)!
(
!
)1
(
i ni
C
i
n
i
.
Здесь
t
=(0,1157-0,101)/0,005=2,94
.
Вычисления располагаем в табл.
4.11.
Таблица 4.11
Результаты вычислений
i
i
x
i
y
i t
i
C
i
C
i t
) (
i
i
C
i t
y
) (
0 0,101 1,26183
2,94
-120
-352,8
-0,0035766
1 0,106 1,27644
1,94
24
46,56
0,0274149
2 0,111 1,29122
0,94
-12
-11,28
-0,1144691
3 0,116 1,30617
-0,06
12
-0,72
-1,8141250
4 0,121 1,32130
-1,06
-24
25,44
0,0519379
5 0,126 1,32660
-2,06
120
-247,2
-0,0054069
Итак,
7024271
,0 )(
15
t
,
858225 ,1
) (
5
0
i
i
i
Ci t
y
. Следовательно,
30527 ,1 )
858225 ,1(
7024271
,0
) (
)
(
)
1157
,0(
5
0
15
i
i
i
Ci t
y
t
f
.
Пример 4.7
Используя интерполяционные формулы Гаусса, вычислить
приближенные значения функции
у
(
х
) при
х=
0,168
и
х=
0,175
.
Таблица 4.12
Исходные данные
х
у
0,12
6,278
0,14
6,404
0,16
6,487
0,18
6,505
0,20
6,436
0,22
6,259
0,24
5,954


