141
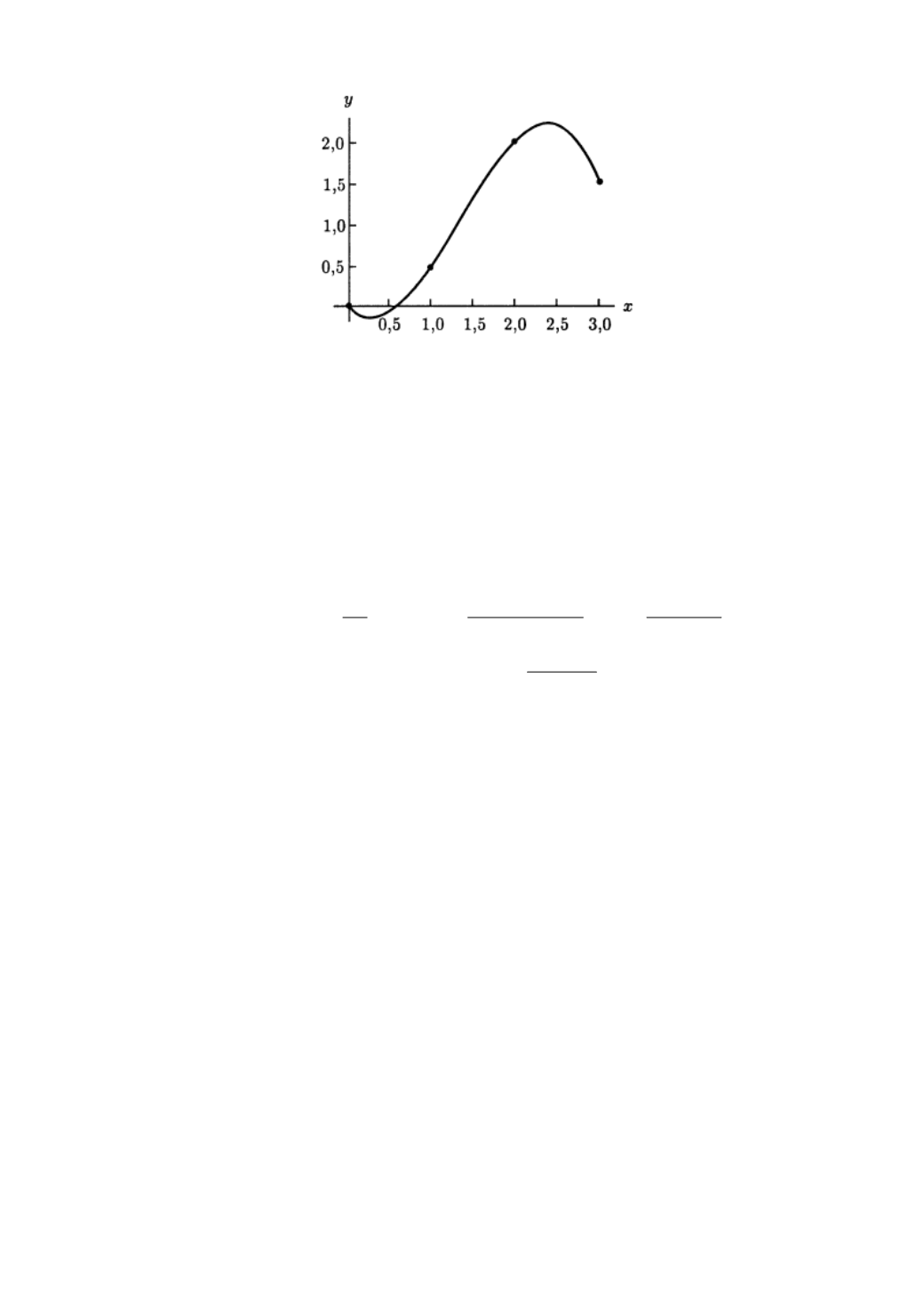
Рис. 4.18. Экстраполяционный кубический сплайн
Пример 4.12
Найти кубический сплайн, заканчивающийся параболой, проходящий
через точки:
(0;0), (1;0,5), (2;2), (3;1,5).
Решение. Кубический сплайн состоит из кубических полиномов:
3
3,
2
2,
1,
0,
)
(
)
(
)
(
)(
)
(
k
k
k
k
k
k
k
k
x x s
x x
s
xx
s s
x
S x
S
, где
1
0
N
k
;
N
количество точек (
х
к
, у
к
);
1
k
k
x
x x
.
Коэффициенты сплайна
)(
xS
вычисляются по формулам:
k
k
y
s
0,
,
2
1,
k
k
m
s
,
6
)
2(
1
2,
k
k
k
k
k
mm h
d
s
,
k
k
k
k
h
m m
s
6
1
3,
,
(4.60)
где
) (
"
k
k
x
S m
,
)
("
1
1
k
k
x
S
m
,
k
k
k
x x h
1
,
k
k
k
k
h
y y
d
1
.
Для вычисления
k
m
применяется следующая формула:
k
k k
k k
k
k
k
u mh mh h
mh
1
1
1 1
)
(2
,
(4.61)
где
)
(6
1
k
k
k
d d
u
для
2 ,...2,1
N k
.
Система (4.61) является линейной системой с
N
-2 уравнениямии
N
неизвестными.
Для кубического сплайна, заканчивающегося параболой, дополняем
ее уравнениями:
.
,
2
1
1
0
N
N
m m
m m
(4.62)
Сначала вычислим величины:
.12 )5,1
5,0(6 )
(6
,6 )5,05,1(6 )
(6
,5,0 1/)25,1(
/)
(
,5,11/)5,02(
/)
(
,5,01/)05,0(
/)
(
,1
1
2
2
0
1
1
2
2
3
2
1
1
2
1
0
0
1
0
2
1
0
d d u
d d u
h y y d
h y y d
h y y d
h h
h
Из системы (4.61) получим уравнения:


