135
Таблица 4.14
Исходные данные
х
у
0
1,5
0,5
0
1
0
2
2
3
2
4
1
5
2
Решение. Осуществим кусочно-линейное
интерполирование. Для этого разобьем
данную функцию на элементарные
промежутки, определяемые соседними
числами первого столбца таблицы –
х
к
, и
на каждом из этих участков построим
интерполяционный полином Лагранжа
первой степени (прямую линию):
k
k
k
k
k
k
k
k
k
x x
x x
y
x x
x x
y x
S
1
1
1
1
)
(
.
В результате получим
.5
4 при
3
,3
3
при 5
,3
2 при
2
,2
1 при
2 2
,1
0,5
при
0
,5,0
0 при 5,1 3
)(
1
x
x
x
x
x
x
x
x
х
х
x
S
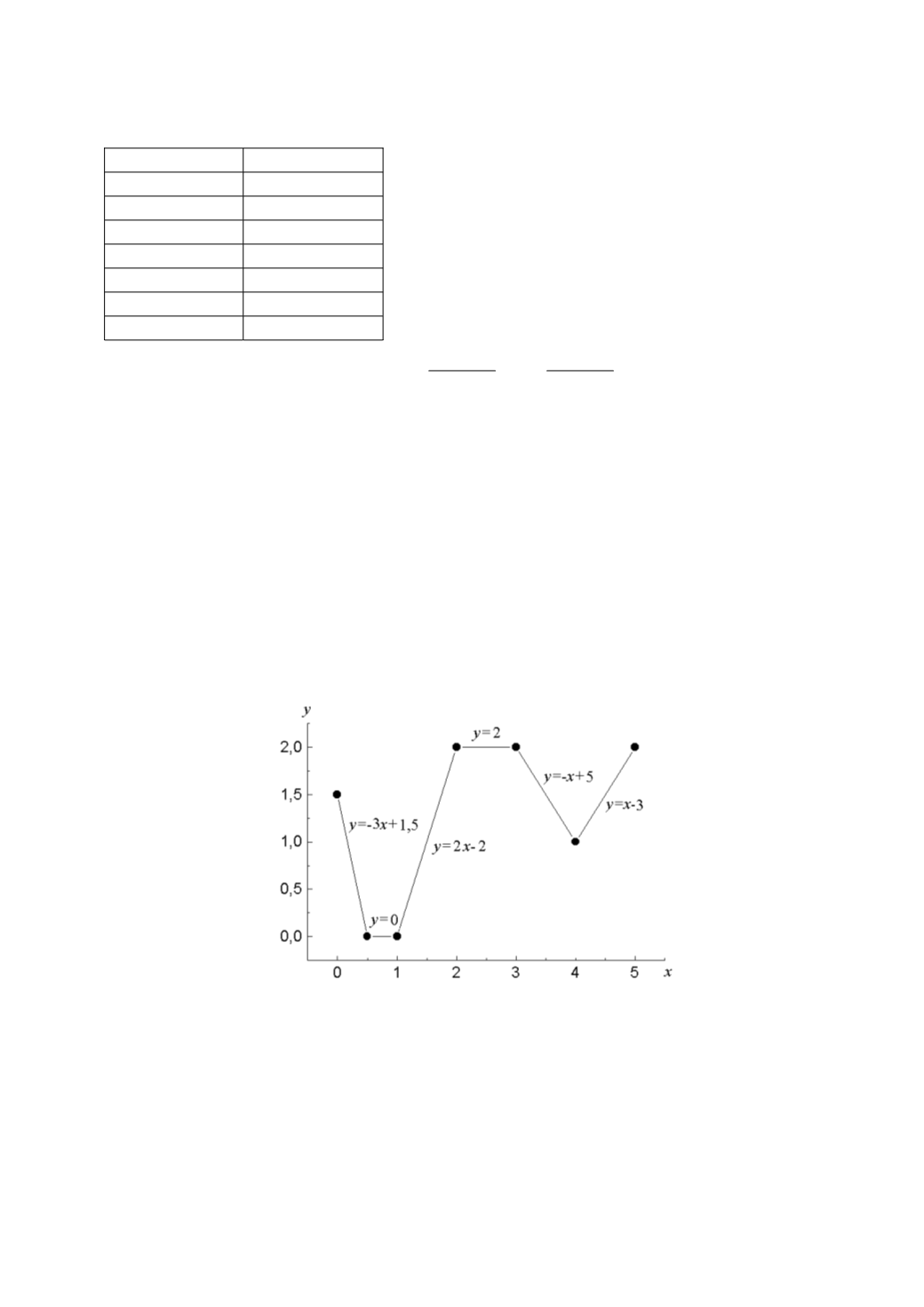
График
полученного
кусочно-линейного
интерполирования
представлен на рис. 4.14.
Рис. 4.14. Кусочно-линейная интерполяция
Осуществим кусочно-квадратичное интерполирование. Для этого
будем рассматривать тройки известных точек отрезков [0;1], [1;3], [3;5].
На каждом из этих отрезков по известным точкам построим полином
Лагранжа второй степени (параболу):


