102
.
)1 (
)1
(
)
( )
(
]2 [
2
]2 [
]1 [
][
]
[ 2
n
n
n
n
n
x n
nh
hx n nh
nhx
x
x
Итак,
]2 [
2
]
[ 2
)1 (
n
n
xh
nn x
.
Методом математической индукции легко доказать общую формулу
,
)]1 (
)...[ 1 (
]
[
][
kn k
n k
xh k n
nn x
где
.
,..., 2,1
n
k
Очевидно,
∆
k
х
[
п
]
= 0 при
k
>
n
.
Из формулы (4.12) вытекает также простая формула
конечного
суммирования.
Пусть
x
0
, x
1
, x
2
, ...
равноотстоящие точки с шагом
h:
x
i+
1
– x
i
=h
(
i =
0, 1, 2 . . . ) .
Рассмотрим сумму
1
0
][
N
i
n
i
N
x
S
. Так как в силу формулы (4.12) имеем
)1 (
]1 [
][
nh
x
x
n
n
, то
)1
(
1
0
1
1
0
][
n
h
x
x
x
S
n
n
N
N
i
n
i
N
.
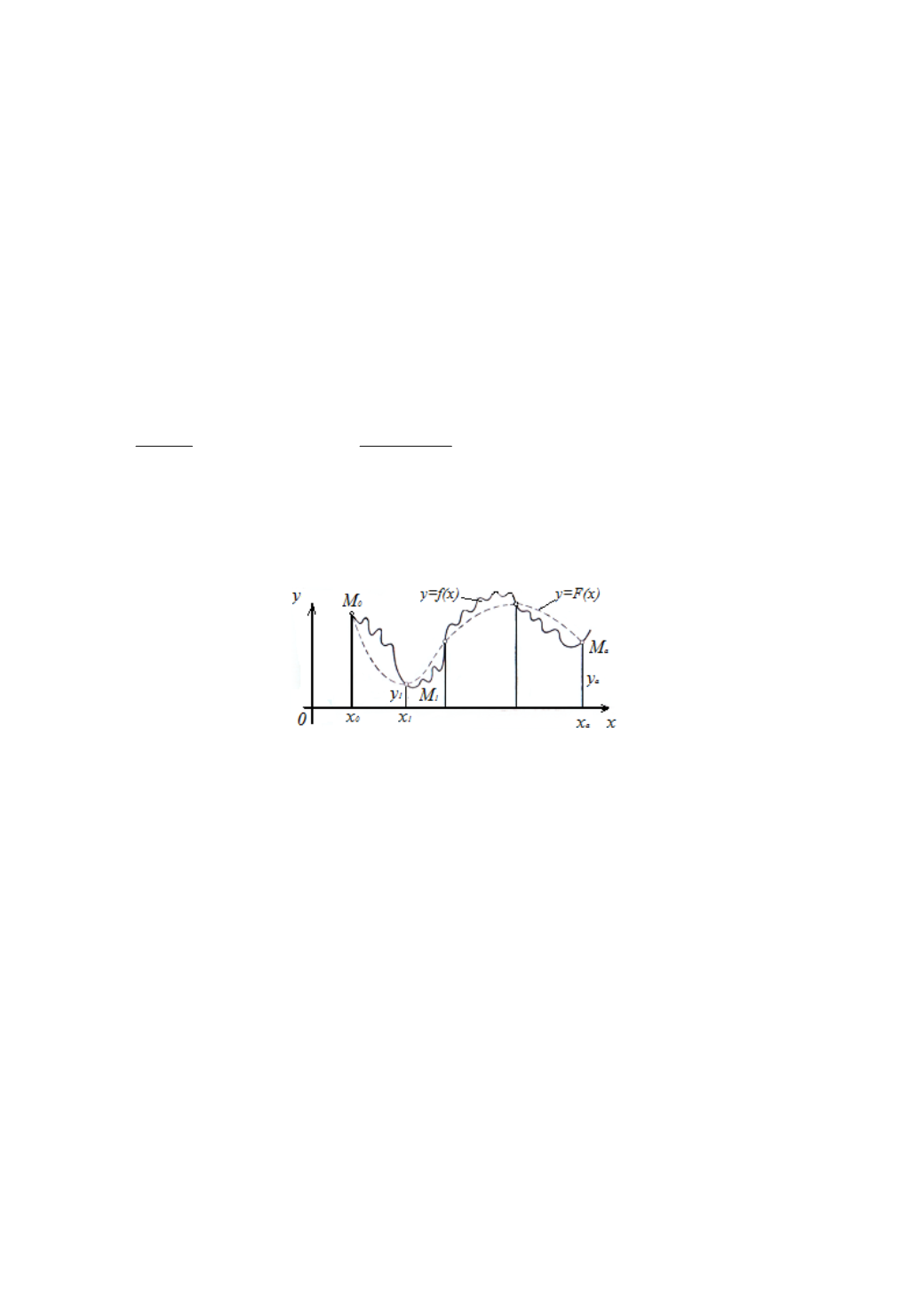
4.4. Постановка задачи интерполирования
Рис. 4.1. Постановка задачи интерполирования
Простейшая задача интерполирования заключается в следующем. На
отрезке [
а,b
] заданы
n
+1 точки
х
0
,
х
1
, ... ,
х
n
,
которые называются
узлами
интерполяции,
и значения некоторой функции
f
(
х
) в этих точках
f
(
x
0
)=y
0
,
f
(
x
1
)=y
1
, ... ,
f
(
x
n
)=y
n
.
(4.13)
Требуется построить функцию
F
(
х
)
(интерполирующая функция),
принадлежащую известному классу и принимающую в узлах
интерполяции те же значения, что и
f
(
х
), т. е. такую, что
F(x
0
)=
y
0
,
F
(
x
1
)=
y
1
, ...,
F
(
x
n
)=
y
n
.
(4.14)
Геометрически это обозначает, что нужно найти кривую
у = F(х)
некоторого определенного типа, проходящую через заданную систему
точек
M
i
(
x
i
,
y
i
) (
i =
0, 1, 2, ...) (рис. 4.1).
В такой общей постановке задача может иметь бесчисленное
множество решений или совсем их не иметь. Однако эта задача


