92
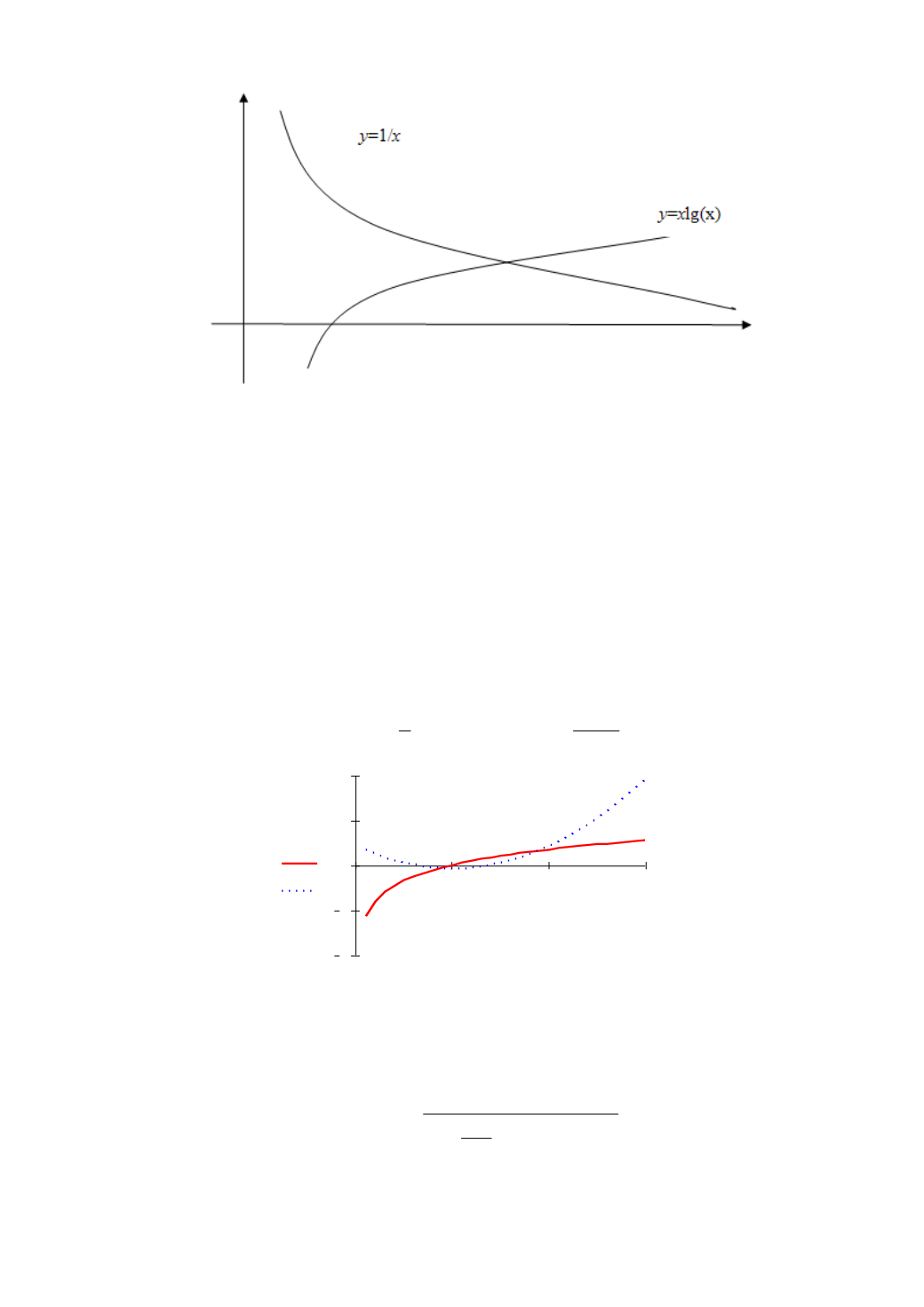
Рис. 3.20. Графическое решение уравнения
Пример 3.7
С помощью графического метода отделить корни трансцендентного
уравнения и уточнить их методом Ньютона с точностью
=0,00001:
0
15
,0 )1
( )
ln(
2
x
x
.
Решение
.
Запишем наше уравнение в виде
2
1
y y
, где
)
ln(
1
x
y
;
15,0 )1 (
2
2
x y
. Строим графики данных функций.
Из рис. 3.21 видно, что данное уравнение имеет два корня: первый
корень принадлежит отрезку [0.1; 1], а второй [1.1; 2].
Уточним корни методом касательных. Для этого вычислим
производные
1 2
1
)(
x
x
x f
;
2
1
)(
2
x
x
f
.
0
1
2
3
4
2
2
4
y1 x( )
y2 x( )
x
Рис. 3.21. Графический метод отделения корней
трансцендентного уравнения
Итерационная формула метода Ньютона в данном случае имеет вид
1
2
1
15,0 )1 ( )
ln(
1
1
2
1
1
1
n
n
n
n
n
n
x
x
x
x
x x
,
где
n
= 1, 2, 3, …
.


