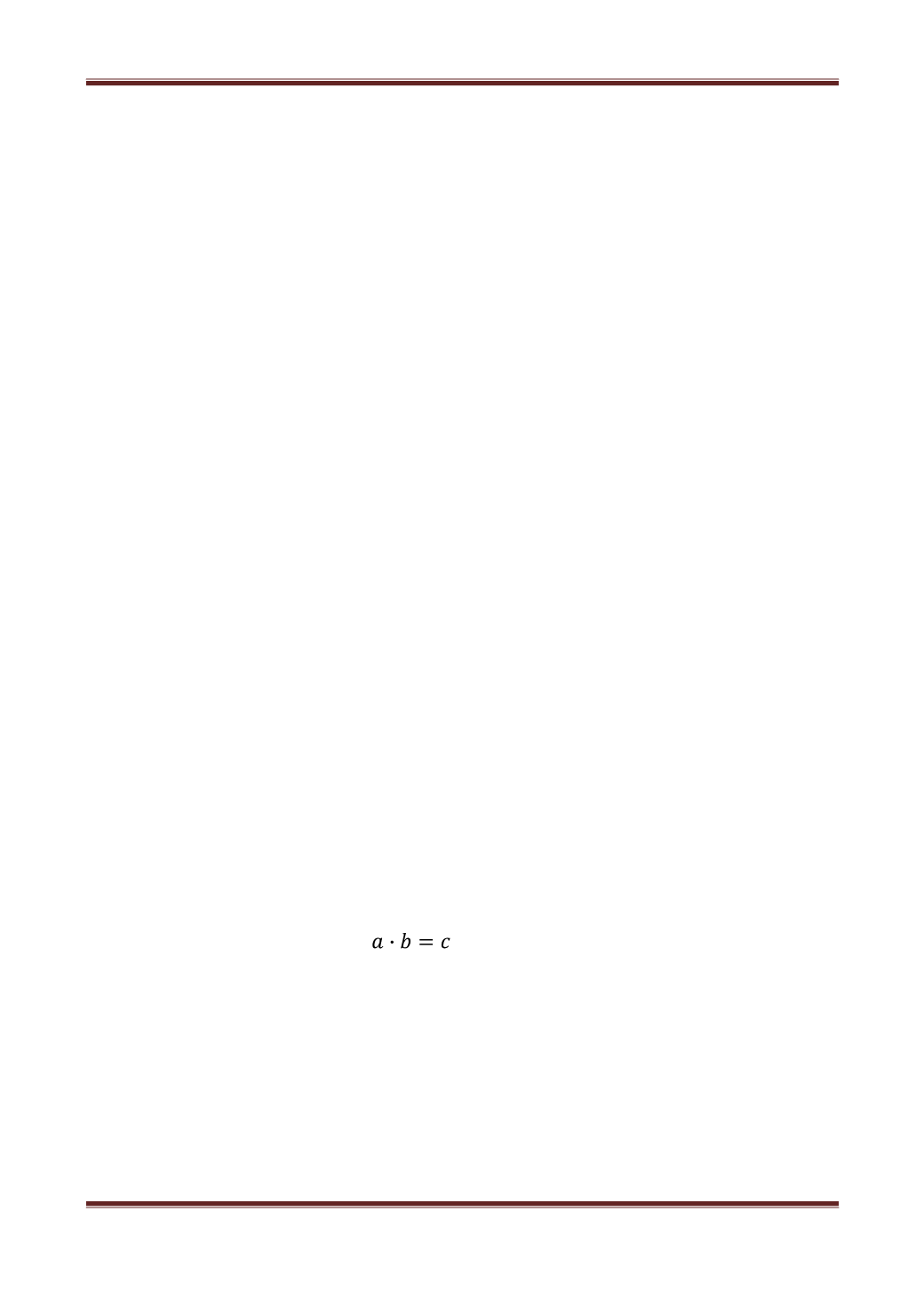
" Н а у к а м о л о д ы х " , 3 0 - 3 1 м а р т а 2 0 1 7 г . , А р з а м а с
П о с в я щ а е т с я 1 0 0 - л е т и ю Р о с т и с л а в а Е в г е н ь е в и ч а А л е к с е е в а
698
задачами на движение учащиеся знакомятся ещё в начальной школе, но, к
сожалению, эта тема вызывает трудности у учащихся на протяжении всего
школьного курса математики. У учащихся часто отсутствуют навыки
выделения из текста необходимых им условий и вопроса задачи.
Возможно, данная тенденция наблюдается из-за смещения акцента с
процесса математического моделирования, рассмотренной в задаче ситуации,
на отработку математических алгоритмов.
Для решения данной проблемы, возможно, целесообразно рассмотрение
на уроках математики задач не из учебника, а моделирование реальных
ситуаций из жизни учащихся и совместное формулирование проблемы и поиск
пути ее решения. Также для актуализации математических знаний необходимо
уделять на уроке время для демонстрации применения изученных понятий в
привычных и повседневных вещах.
Задачи по данной теме можно разделить на три основные группы:
1.
Задачи, которые направлены на элементарное применение
формулы.
2.
Задачи на встречное движение или на со-направленное движение.
3.
Задачи на движение по кругу.
Для вовлечения учащихся в процесс решения задачи, продуктивно
создать проблемную ситуацию, из которой ученик вынужден искать выход.
Таким образом, учитель может предлагать ученикам различные жизненные
ситуации, которые можно математически смоделировать.
Например, предложить ученикам временно стать пассажирами двух
поездов. В распоряжении учеников есть карта движения поездов, на которой
отмечены точки отправления и точка, в которой две группы должны
соединиться. Одна группа может ожидать вторую не более одного часа (или
группы должны прибыть в пункт назначение одновременно). Далее ученикам
предлагается определить необходимые условия, чтобы такая встреча
состоялась.
В данной задаче ученики могут измерить путь каждого поезда по
предложенной карте (желательно чтобы пути были различны по длине), а далее
они должны сами понять, какие данные им еще потребуются и как ими можно
оперировать. Такая ситуация вынуждает учеников прибегнуть к известному им
математическому отношению
.
В процессе решения и обсуждения задачи у преподавателя есть
возможность ставить дополнительные ограничения на движение поездов, чтобы
создать условия, при которых учащиеся будут вынуждены искать новый путь
решения проблемы. Например, первый поезд, пройдя треть пути начал
двигаться в два раза медленнее из-за плохих погодных условий или оба поезда
должны выехать из пунктов отправления одновременно. Также полезно сделать
время движения поездов равным одному часу, в таком случае скорость
получается численно равной пройденному пути, что часто вводит в
замешательство учащихся.