76
Возможен также другой вид ломаной
...
2 2 1
1 0
ABA
BA
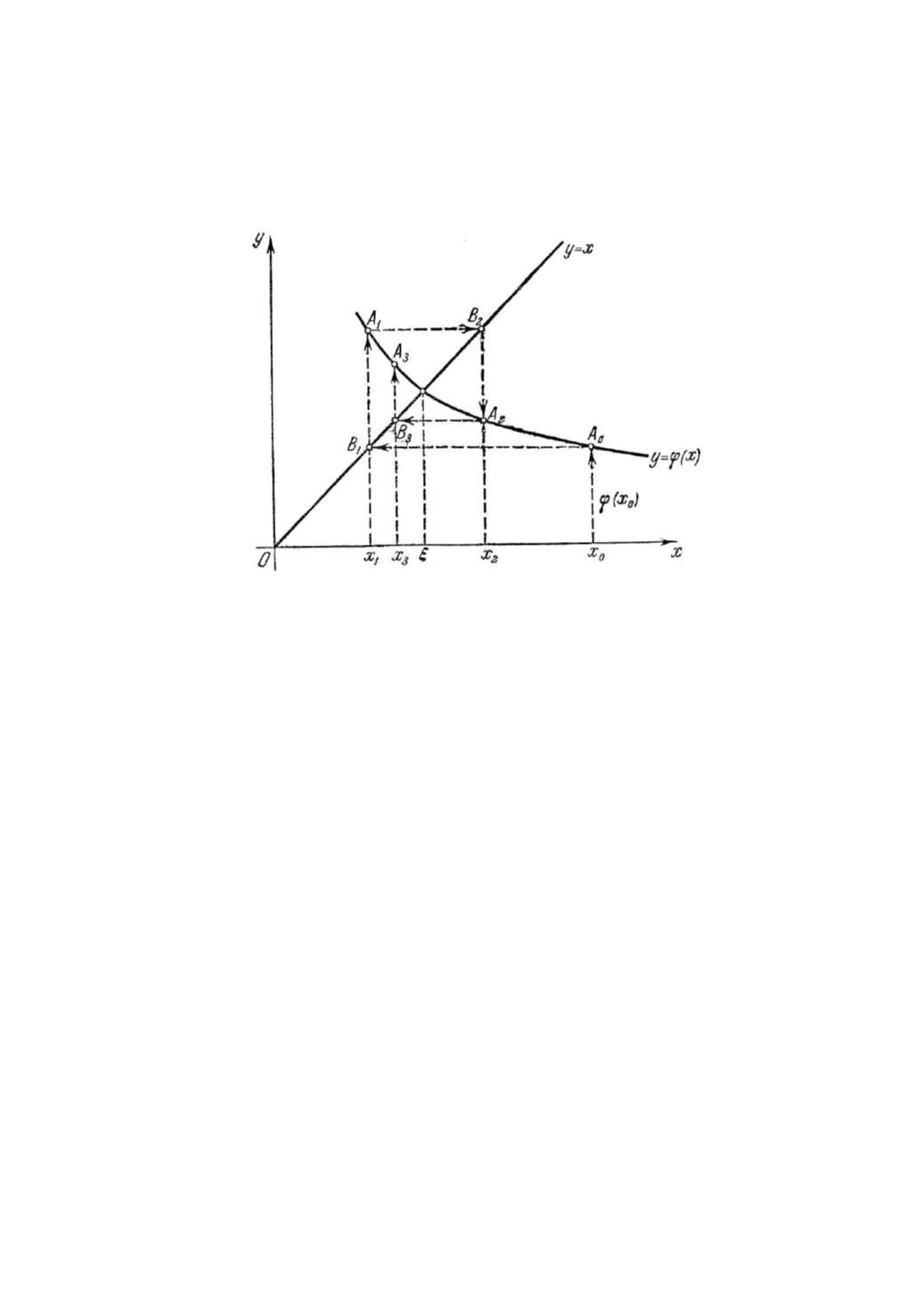
«спираль». Легко
сообразить, что решение в виде «лестницы» получается, если
производная
’(
x
) положительна, а решение в виде «спирали», если
’(
x
)
отрицательна (рис. 3.3).
Рис. 3.3. Графическая интерпретация метода итераций вида «спираль»
На рисунке с «лестницей» кривая
y
=
(
x
) в окрестности
– пологая,
т.е. |
’(
x
)|<1 и процесс сходится. Однако, если рассмотреть случай, где
|
’(
x
)|>1, то процесс итерации может быть расходящимся. Поэтому для
практического применения метода итерации нужно выяснить
достаточные условия сходимости итерационного метода.
Теорема 1.
Пусть функция
(
x
)
определена и дифференцируема на
отрезке
[
a
,
b
],
причем все ее значения
(
x
)
[
a
,
b
].
Тогда, если существует
правильная дробь q такая, что
|
’(
x
)
|
≤
q
<1
(3.15)
при
,
bx
a
процесс итерации
x
n
=
(
x
n
-1
) (
n
= 1,2,…)
(3.16)
сходится, независимо от начального значения
; ,
0
ba
x
предельное значение
n
n
x
lim ξ
является единственным корнем уравнения
x
=
(
x
)
(3.17)
на отрезке
.
,
ba
Доказательство
. Рассмотрим два последовательных приближения
x
n
=
(
x
n
-1
) и
x
n
+1
=
(
x
n
), которые в силу условий теоремы заведомо имеют
смысл. Отсюда
x
n
+1
x
n
=
(
x
n
)
(
x
n
-1
)
.


