75
Выберем каким-либо грубо приближенное значение корня
0
x
и
подставим его в правую часть уравнения (3.11). Тогда получим некоторое
число
).
(
0
1
x
x
(3.12)
Подставляя теперь в правую часть равенства (3.12) вместо
x
0
число
x
1
получим новое число
x
2
=
(
x
1
)
.
Повторяя это процесс, будем иметь
последовательность чисел
x
n
=
(
x
n
-1
) (
n
= 1, 2,…).
(3.13)
Если эта последовательность – сходящаяся, т.е. существует
n
n
x
lim
ξ
,
то, переходя к пределу в равенстве (3.13) и предполагая функцию
(
x
)
непрерывной, найдем
n
n
x
lim
)
lim(
1
n
n
x
или
ξ
)
ξ
(
.
(3.14)
Таким образом, предел
является корнем уравнения (3.11) и может
быть вычислен по формуле (3.13) с любой степенью точности.
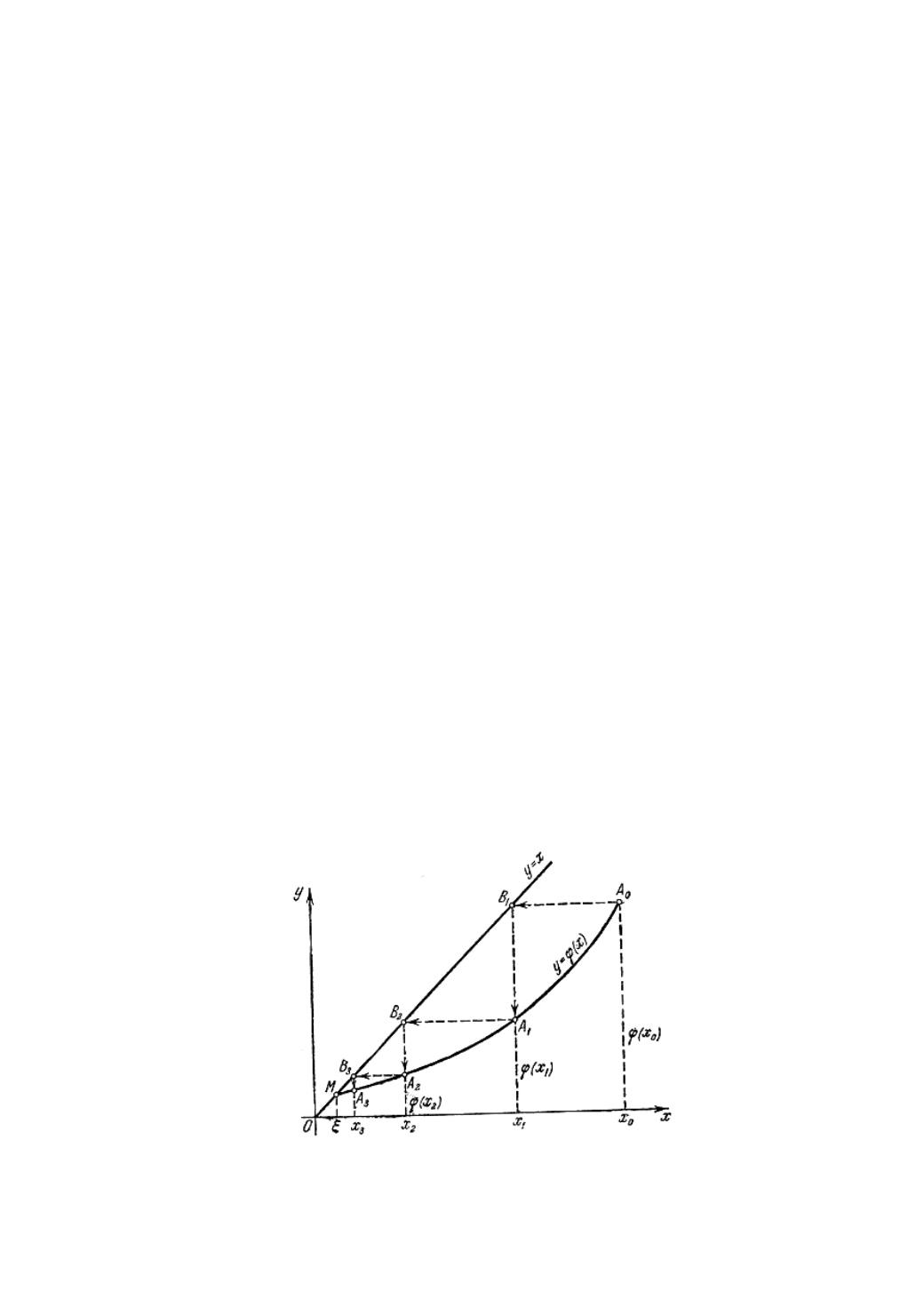
Геометрически способ итерации может быть пояснен следующим
образом (рис. 3.2). Построим на плоскости
xOy
графики функций
y
=
x
и
y
=
(
x
). Каждый действительный корень
уравнения (3.11) является
абсциссой точки пересечения
M
кривой
y
=
(
x
) с прямой
y
=
x
.
Отправляясь от некоторой точки
) (
;
0
0 0
x
x
A
,
строим ломаную линию
...
2 2 1 1
0
ABABA
«лестница», звенья которой попеременно параллельны оси
Ox
и оси
,
Oy
вершины
...
,
,
2 1 0
AA
A
лежат на кривой
y
=
(
x
) а вершины
...
,
,
2 1 0
B
B
B
– на прямой
y
=
x.
Общие абсциссы точек
1
A
и
,...,
,
,
2
2
1
BAB
очевидно,
представляют собой соответственно последовательные приближения
,...
,
2
1
xx
корня
.
Рис. 3.2. Графическая интерпретация метода итераций вида «лестница»


