73
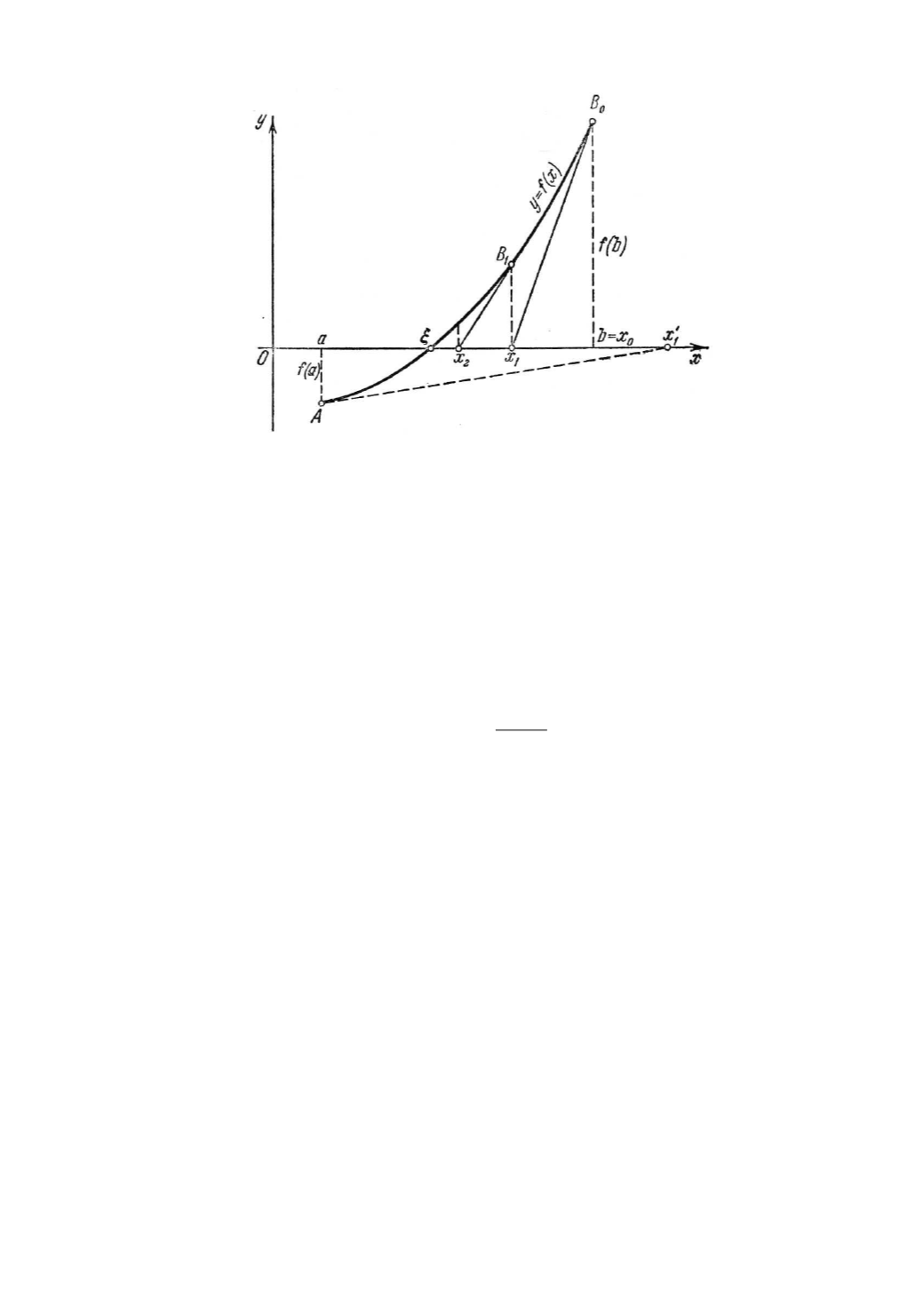
Рис. 3.1. Графическая интерпретация метода Ньютона
В качестве первого приближения
1
x
корня
возьмем абсциссу точки
пересечения этой касательной с осью
.
Ox
Через точку
)
(
,
1
1 1
xf
xB
снова
проведем касательную, абсцисса точки пересечения которой дает нам
второе приближение
2
x
корня
и т.д. Очевидно, что уравнение
касательной в точке
,...) 2,1,0 ( ) ( ,
n xf xB
n
n n
есть
).
)( (
)
(
n
n
n
x
x
x f
xf
y
Полагая
,
,0
1
n
x x y
получим формулу (3.7)
.
)
(
) (
1
n
n
n
n
x
f
x
f
x x
Заметим, что если в нашем случае положить
a x
0
и, следовательно,
,0 ) ( ) (
0
0
x
f
xf
то, проведя касательную к кривой
)
(
xf
y
в точке
,
)
(
,
af
a
A
мы получили бы точку
1
x
, лежащую вне отрезка
ba
,
, т.е. при выборе
начального значения метод Ньютона оказывается непрактичным. Таким
образом, в данном случае «хорошим» начальным приближением
0
x
является то, для которого выполнено неравенство
.0
)
(
)
(
0
0
x
f
x
f
(3.8)
Докажем, что это правило является общим.
Теорема
. Если
,0
)
(
)(
bfaf
причем
)(
x f
и
)(
x f
отличны от нуля и
сохраняют определенные знаки на
,
b x
a
то, исходя из начального
приближения
, ,
0
ba x
удовлетворяющего неравенству (3.8), можно
вычислить методом Ньютона (формула (3.7)) единственный корень
уравнения (3.5) с любой точностью.


