119
Пусть общее количество точек равно
m
. Обозначим
i
отклонение
i
-й
точки от искомой прямой:
i
=
(
x
i
)
– y
i
.
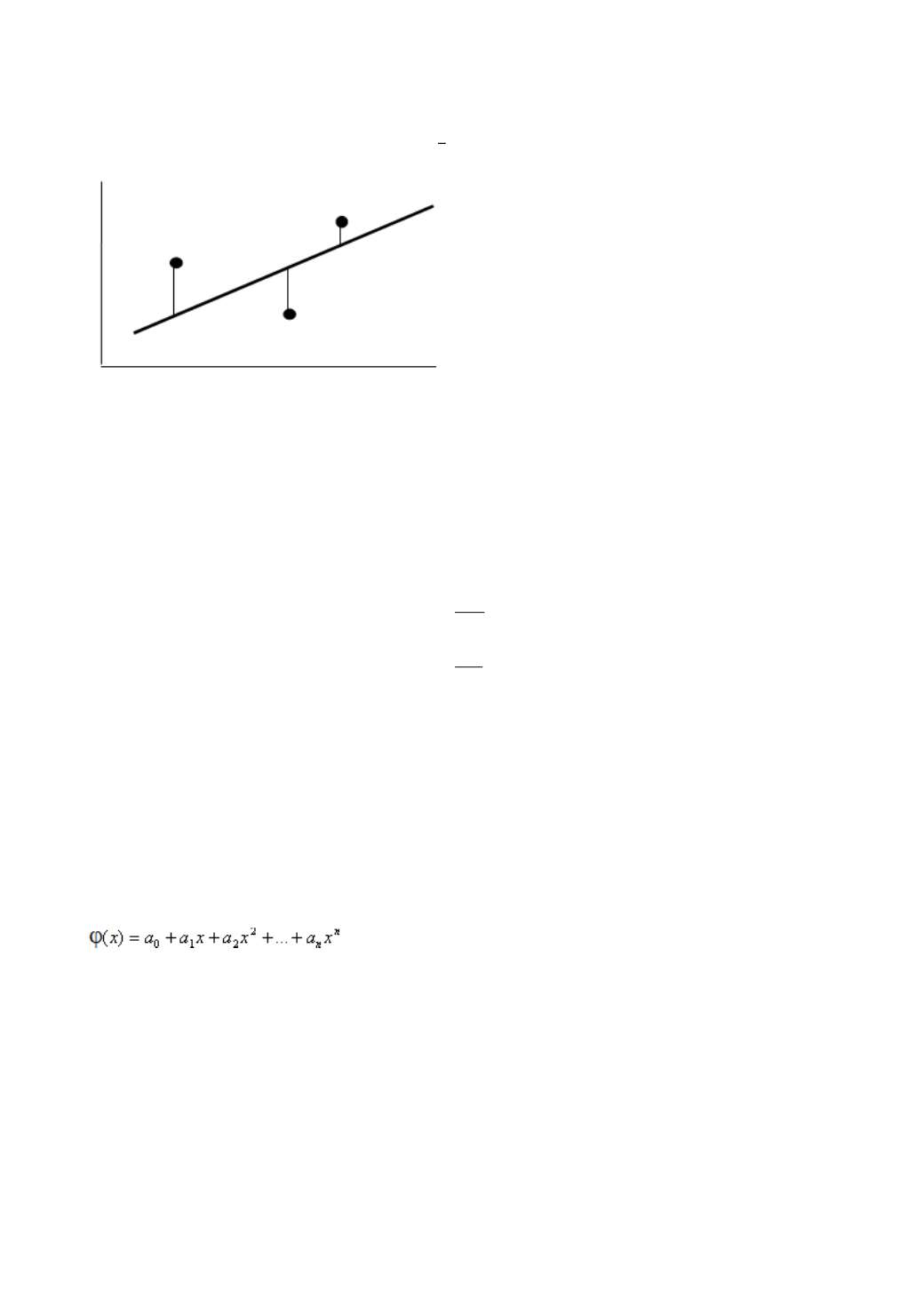
Рис. 4.4 Отклонения
Как видно из рис. 4.4,
отклонения
могут
быть
как
положительными,
так
и
отрицательными.
Чтобы
определить
близость
искомой
функции к табличным точкам,
необходимо
составить
сумму
квадратов всех отклонений.
Метод наименьших квадратов заключается в минимизации суммы
квадратов отклонений. В нашем случае эта функция равна:
m
i
i
i
m
i
i
y xa a
S
1
2
1
0
1
2
.
Для нахождения минимума функции
S
необходимо приравнять нулю
ее частные производные. В результате получим систему уравнений:
.0
,0
1
0
a
S
a
S
Опуская промежуточные преобразования, получим систему уравнений
для нахождения неизвестных коэффициентов
a
0
и
a
1
:
.
,
1
2
0
1
0
i i
i
i
i
i
y
x
a
x
a
x
y
ax
ma
где
m
– количество точек; суммирование здесь и далее предполагается по
всем точкам (
i =
1, 2,…,
m
).
Метод наименьших квадратов несложно распространить на общий
случай, когда мы будем искать функцию
(
x
) в виде полинома степени
n
:
.
Отметим, что в случае аппроксимации всегда справедливо
следующее соотношение, связывающее количество исходных точек
m
и
степень искомого полинома
n
m
– 1
, причем в случае равенства мы
приходим к интерполяции (все отклонения равны нулю).
Неизвестные коэффициенты
a
0
,
a
1
, …,
a
n
находим из условия
минимизации суммы квадратов отклонений искомой функции от
исходных точек. По аналогии с полиномом первой степени в нашем
случае имеем систему уравнений:
ZA = B
, где
Z -
квадратная матрица
размерностью (
n
+1)
(
n
+1), составленная из известных координат точек;


