Модели в инновационной экономике - page 90

88
Выходной поток заявок связан с потоком обслуживания в канале, где
длительность обслуживания tобс является тоже случайной величиной и подчи-
няется во многих случаях показательному закону распределения с плотностью
вероятности:
, μν ) ( μ обс t
обс e tf 

где   интенсивность потока обслуживания, т.е. среднее число заявок, обслу-
живаемых в единицу времени:
,
1
μ
обс t
 обс t  среднее время обслуживания заявок .
Важной характеристикой СМО, объединяющей показатели  и , явля-
ется интенсивность нагрузки:  = /, которая показывает степень согласования
входного и выходного потоков заявок канала обслуживания и определяет
устойчивость системы массового обслуживания.
5.2. Графы состояний СМО
При анализе случайных процессов с дискретными состояниями и непре-
рывным временем удобно пользоваться вариантом схематичного изображения
возможных состояний СМО на рисунке в виде графа с разметкой его возмож-
ных фиксированных состояний. Состояния СМО изображаются обычно либо
прямоугольниками, либо кружками, а возможные направления переходов из
одного состояния в другое ориентированы стрелками, соединяющими эти со-
стояния. Например, размеченный граф состояний одноканальной системы слу-
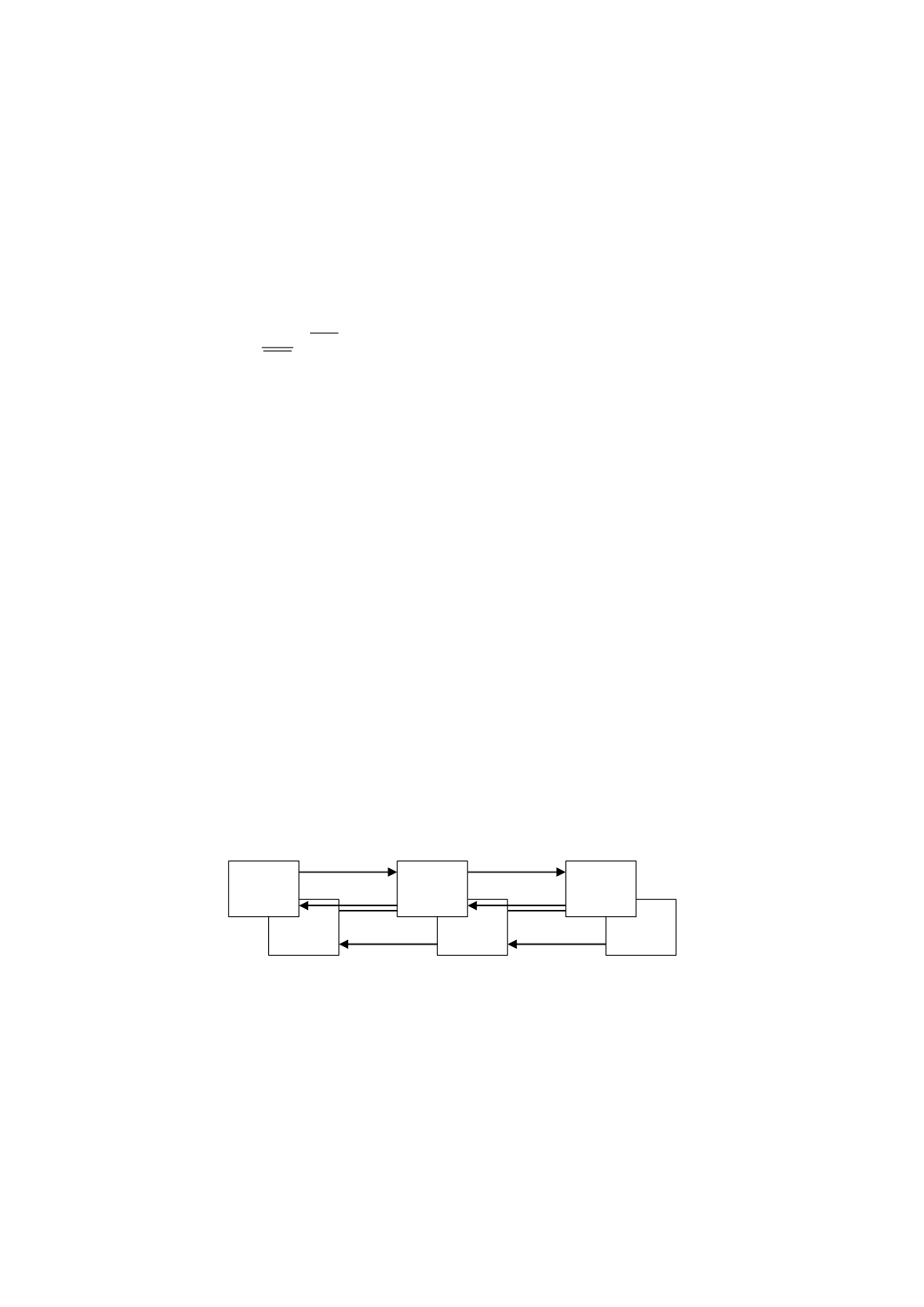
чайного процесса обслуживания в газетном киоске приведен на рис. 5.1.
Рис. 5.1. Размеченный граф состояний СМО
Система может находиться в одном из трех состояний: S0 – канал свобо-
ден, простаивает, S1 – канал занят обслуживанием, S2 – канал занят обслужива-
нием и одна заявка в очереди. Переход системы из состояния S0 в S1 происходит
под воздействием простейшего потока заявок интенсивностью 01, а из состоя-
ния S1 в состояние S0 систему переводит поток обслуживания с интенсивностью
10. Граф состояний системы обслуживания с проставленными интенсивностя-
S0 S1 S2
01 12
21 10
S0 S1 S2
01 12
21 10