118
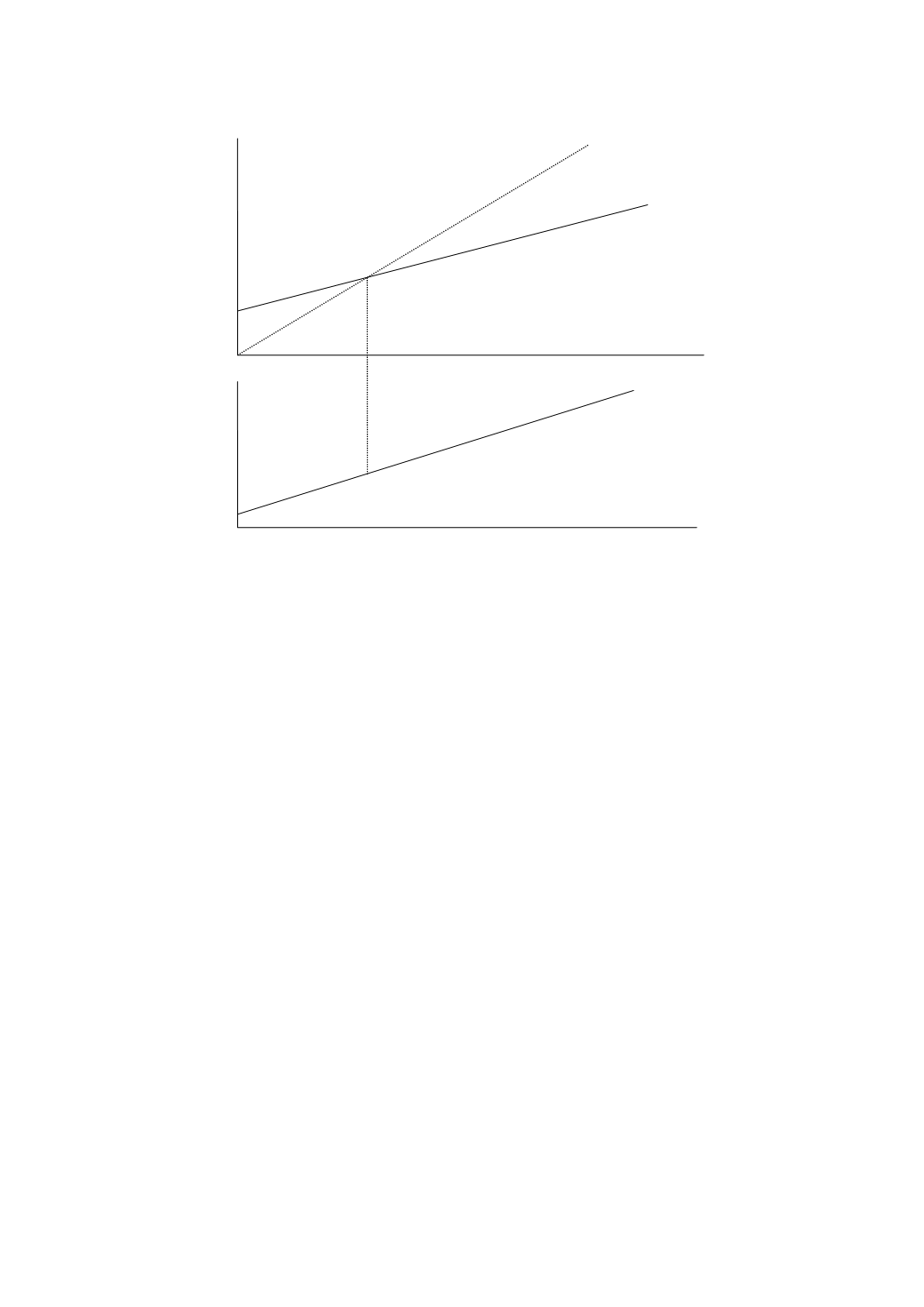
Рис. 6.4. Функции потребления и сбережения (кейнсианский подход)
Пример
.
Пусть
C
= 0,75;
S
= 0,25;
C
0
= 250. Отсюда
S
0
= -250. Имеем
следующие зависимости для функций потребления и сбережения:
C =
250 + 0,75
y
;
S
= -250 + 0,25
y.
Эти зависимости можно изобразить графически (рис. 6.4). В области, где по-
требление превышает доход, сбережения отрицательны, а в области, где доход
превышает потребление – положительны.
Теория потребления с постоянным доходом
Одно из основных следствий двухпериодной модели потребления состо-
ит в том, что потребление домашнего хозяйства зависит не только от текущего
дохода, но и от дохода, который ожидается в будущем. Другими словами, по-
требление в каждом году должно зависеть от среднего уровня дохода, ожидаемо-
го в этом году и в следующие годы. Это положение было впервые сформулиро-
вано в 1950 году лауреатом Нобелевской премией Милтоном Фридменом. Он
использовал термин «перманентный доход», чтобы обозначить средний доход,
который домашние хозяйства ожидают получить в долгосрочной перспективе.
Согласно модели перманентного дохода потребление соответствует до-
ходу
у
р
, который определяется как средняя величина настоящих и будущих до-
ходов. Найдем такое значение
у
р
,
при котором домашнее хозяйство буде иметь
C
250
-250
S
C = y
C
S
y
у


