64
0,01, то решение будет получено за 39 итераций. При точности 0,001
решение получается за 48 итераций.
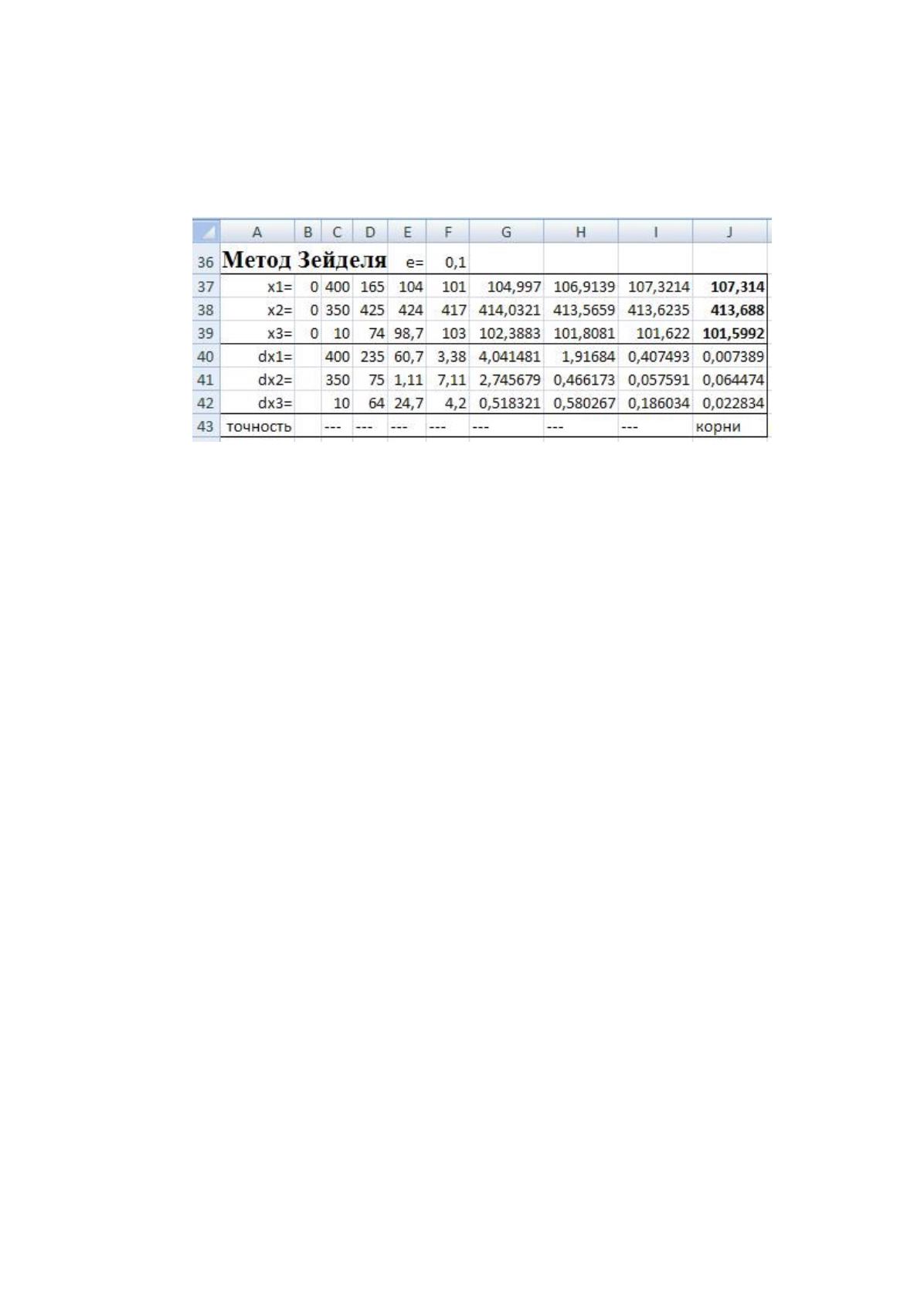
Метод Зейделя. Решение в Microsoft Excel представлен на рис. 2.13.
Рис. 2.13. Метод Зейделя (решение в Microsoft Excel)
Комментарий
. При заданной точности 0,1 решение системы
уравнений получено за 8 итераций. Если задать более высокую точность
0,01, то решение будет получено за 11 итераций. При точности 0,001
решение получается за 12 итераций.
Метод простой итерации, метод Зейделя. Решение в Microsoft Visual Studio
Код программы на языке С++:
// pr1 SLAU ekonom.cpp: определяет точку входа для консольного приложения.
#include
"stdafx.h"
#include
<iostream>
#include
<math.h>
usingnamespace
std;
double
a[3][3]={{6, 4, 1},
{1, 3, 1},
{2, 2, 5}};
double
b[3]={2400, 1450, 1550};
double
x[3]={0, 0, 0};
double
e=0.1;
bool
shod(
double
a[3][3]){
bool
s0=fabs(a[0][0])>fabs(a[0][1])+fabs(a[0][2]);
bool
s1=fabs(a[1][1])>fabs(a[1][0])+fabs(a[1][2]);
bool
s2=fabs(a[2][2])>fabs(a[2][0])+fabs(a[2][1]);
if
(s0 && s1 && s2)
returntrue
;
elsereturnfalse
;
}
bool
toch(
double
b[3],
double
c[3]){
int
i=0;
for
(i=0; i<3; i++){
if
(fabs(b[i]-c[i])>e){
returnfalse
;
}
}
returntrue
;
}


