М а т е р и а л ы X В с е р о с с и й с к о й н а у ч н о - п р а к т и ч е с к о й к о н ф е р е н ц и и
П о с в я щ а е т с я 1 0 0 - л е т и ю Р о с т и с л а в а Е в г е н ь е в и ч а А л е к с е е в а
641
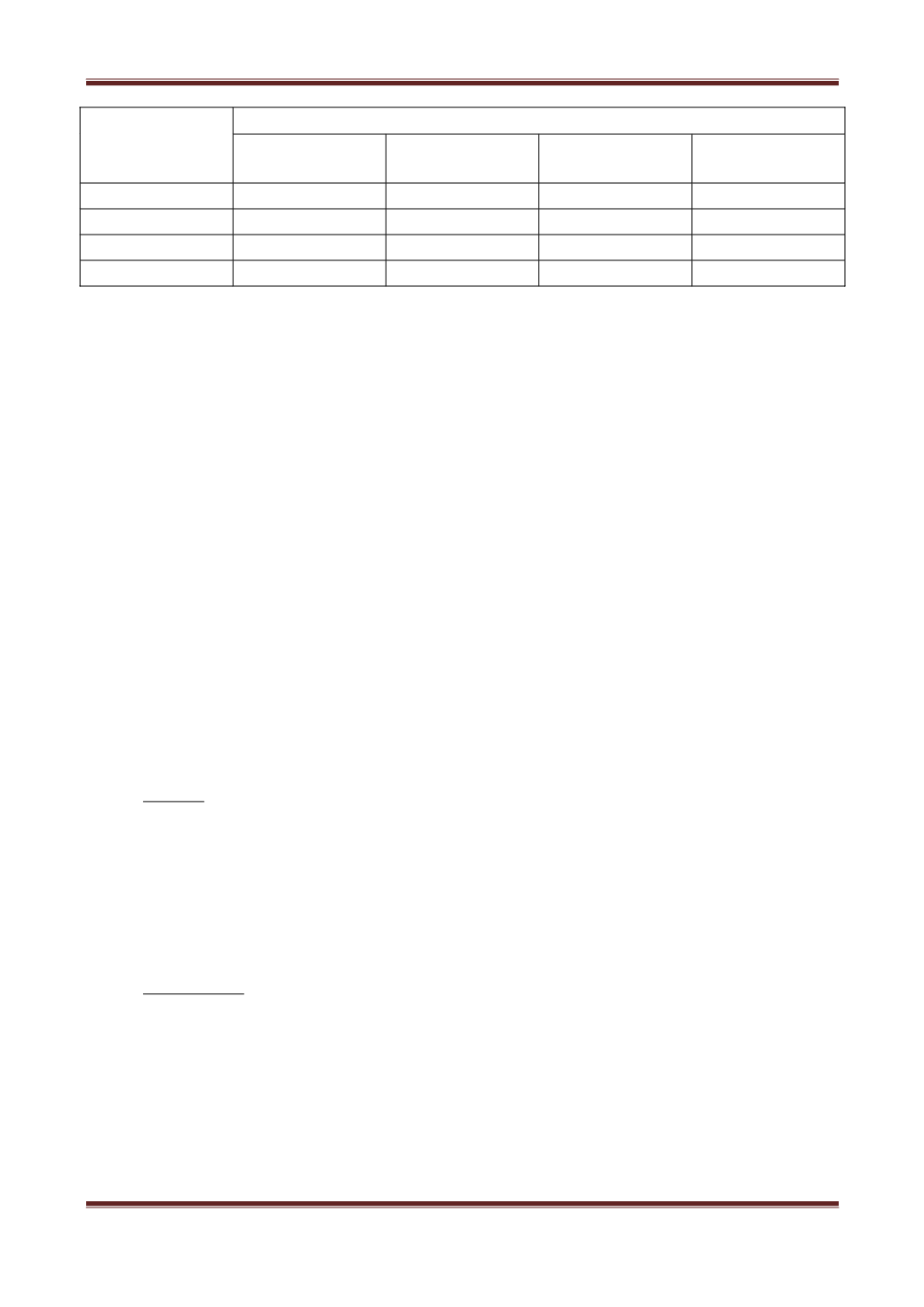
Участник
конкурса
Места
1
2
3
4
А
+
Б
+
+
+
В
+
+
Г
+
Далее начинаем рассуждать: если ошибся конкурсант А, то он занял
второе или третье место. Четвертое место занял конкурсант Г, который
правильно предсказал результат, если ошибся А. Так как по условию задачи
ошибиться может лишь один конкурсант. В этом случае места распределяются
следующим образом:
1) А-2, Б-1, В-3, Г-4
2) А-3, Б-1, В-2, Г-4.
Теперь необходимо доказать, что действительно ошибся конкурсант А и
других вариантов нет. Во-первых, предположим, что ошибся конкурсант Б,
тогда Б занял четвертое место, а это значит, что ошибся и конкурсант Г.
Получаем противоречие с условием задачи. Во-вторых, предположим, что
ошибся конкурсант В, тогда он занял первое или четвертое место. В таком
случае ошибся бы еще один конкурсант или А, или Г. Получаем противоречие с
условием задачи. В-третьих, предположим, что ошибся конкурсант Г, тогда
получаем, что ошибся еще один конкурсант. В противном случае последнее
место не занял бы никто. Получаем противоречие с условием задачи. Таким
образом, других вариантов нет, действительно ошибся конкурсант А.
Ответ: ошибся конкурсант А.
Если в задаче необходимо найти соответствие между элементами
различных множеств, то следует применять
метод моделирования с помощью
графов.
В этом случае элементы различных множеств обозначаются точками, а
соответствия между элементами обозначаются отрезками. Пунктирные отрезки
будут обозначать указанное в задаче отсутствие соотношения. Рассмотрим
применение данного метода при решении следующей задачи.
Задача 4. Три подруги – Елена, Яна и Татьяна преподают различные
предметы (математику, информатику и физику) в школах Новосибирска,
Томска и Барнаула. О них известно следующее:
1)Елена работает не в Новосибирске, а Яна работает не в Барнауле;
2) житель Новосибирска преподает физику;
3) тот, кто работает в Барнауле, преподает математику;
4) Яна и Татьяна преподают не информатику.


