31
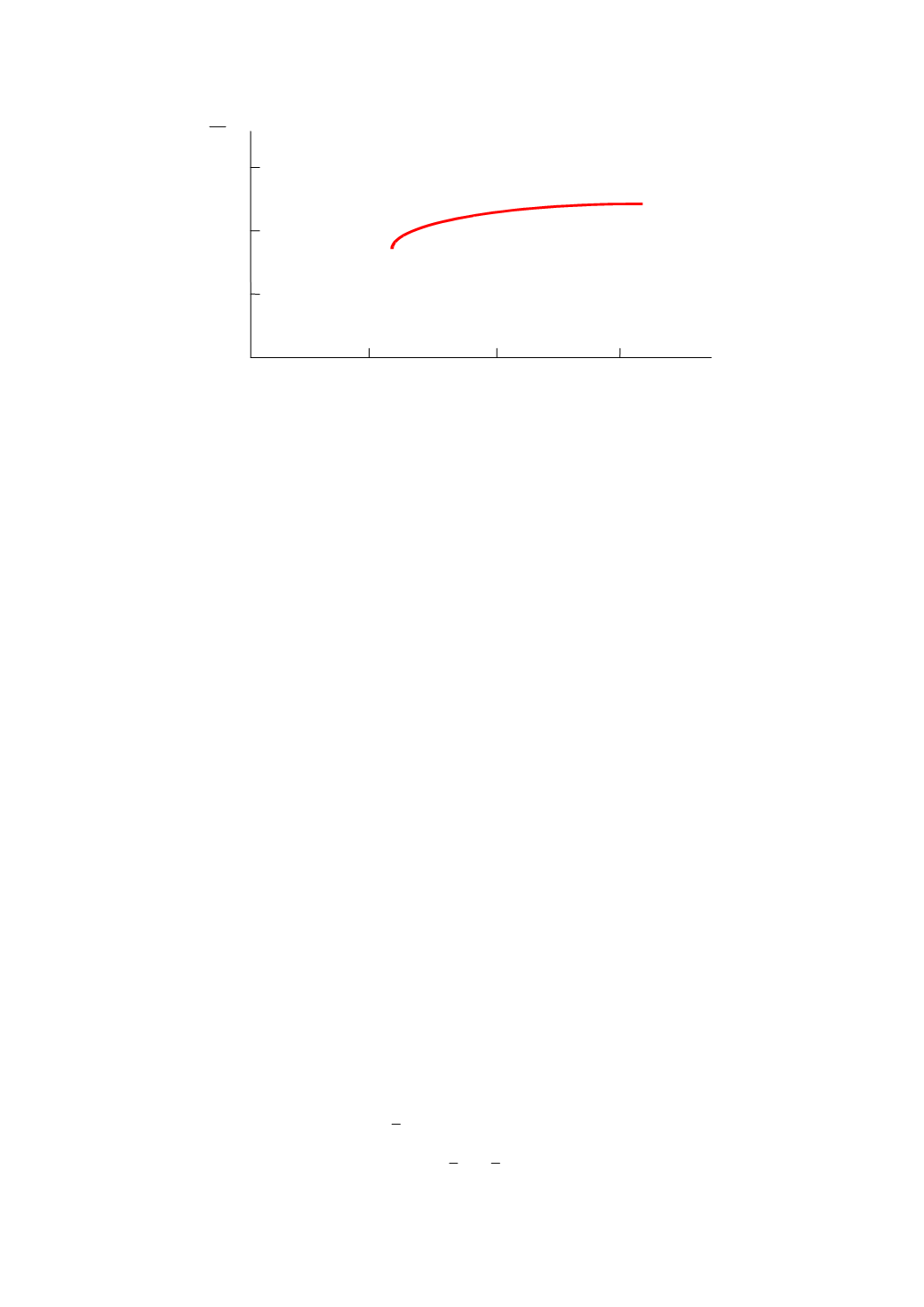
Рис. 2.4. Угловые портфели
Третий портфель имеет следующий состав:
16,0
00,0
84,0
)3(
X
.
Ожидаемая доходность и стандартное отклонение данного портфеля
равны соответственно 17,26 и 12,22%. Как и два предыдущих данный портфель
является эффективным и обозначается на рисунке (3).
Далее алгоритм определяет состав четвертого «углового» портфеля:
01,0
00,0
99.0
)4(
X
.
Можно вычислить его ожидаемую доходность и стандартное отклоне-
ние, которые равны 16,27% и 12,08% соответственно. Определив данный порт-
фель, имеющий наименьшее стандартное отклонение из всех достижимых
портфелей, алгоритм останавливается.
После того как были определены структура и местоположение эффек-
тивного множества Марковица, можно определить состав оптимального порт-
феля инвестора. Этот портфель соответствует точки касания кривых безразли-
чия инвестора с эффективным множеством. Из графика инвестор определяет,
где располагается эта точка и оценивает ожидаемую доходность портфеля. Те-
перь можно определить два «угловых» портфеля с ожидаемыми доходностями,
лежащими выше или ниже данного уровня. Если ожидаемую доходность опти-
мального портфеля обозначить
*
r
, а ожидаемые доходности двух ближайших
«угловых» портфелей соответственно
a
r
и
b
r
, то состав оптимального портфеля
30%
20%
10%
r
p
10%
20%
30%
p
(4)
(3)
(2)
(1)


