34
Мерой доходности комбинации проектов в данном случае является ма-
тематическое ожидание чистой текущей стоимости выбранного портфеля, ко-
торое равно сумме математических ожиданий отдельных чистых текущих сто-
имостей проектов, входящих в портфель:
N
i
i
p
NPV
NPV
1
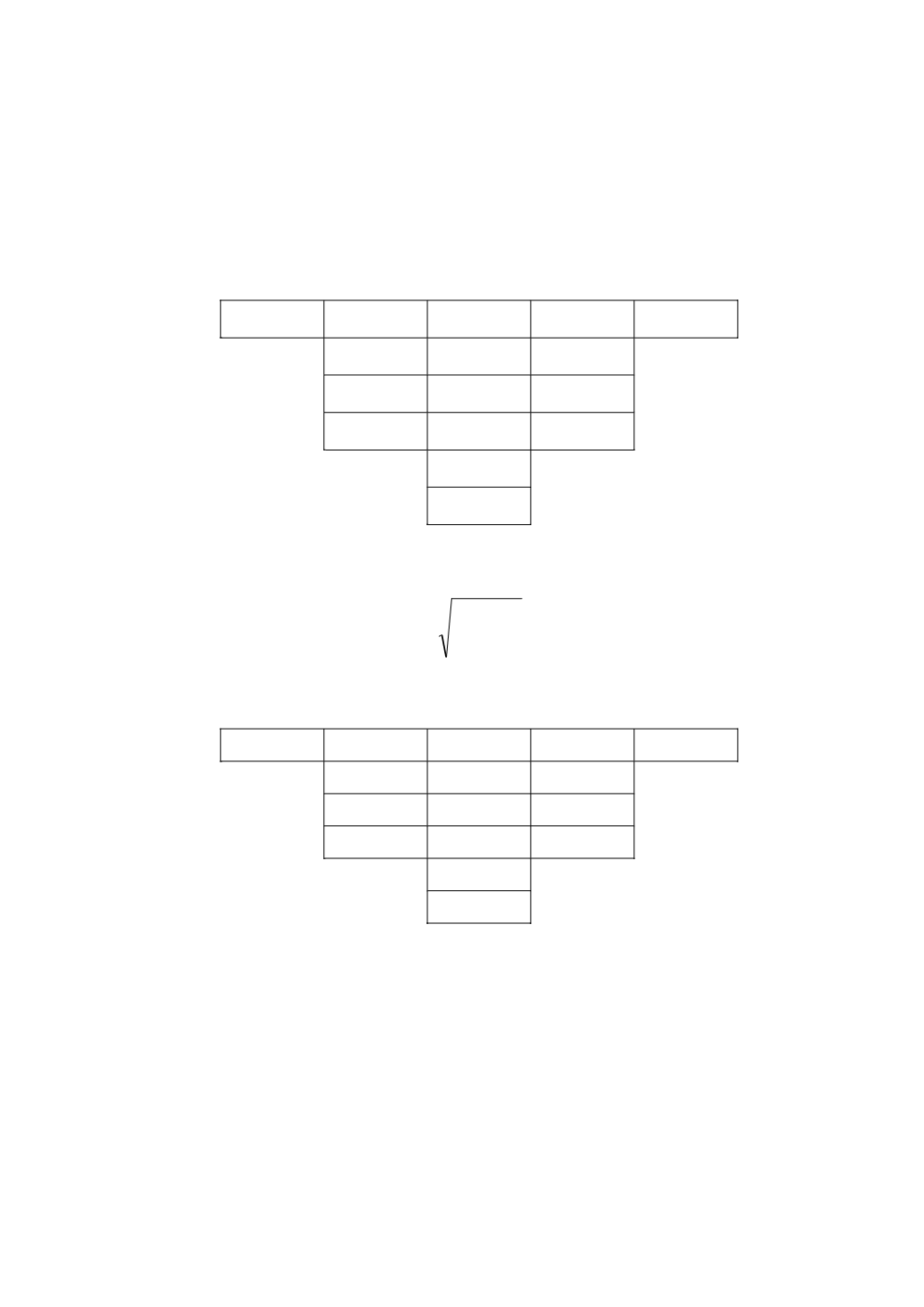
Таблица 2.7. Ожидаемые доходности портфелей проектов
9
1
6
15
15
14
10
6
18
1
10
9
23
23
14
18
Далее вычисляются стандартные отклонения для различных комбинаций
проектов по формуле:
n
i
n
j
ij
p
1
1
σ
σ
.
Таблица 2.8. Стандартные отклонения портфелей проектов
4
2,966
7,057
7,5498
9,4763
7,28
1,000
8,6833
3,256
5,138
5,0794
5,586
7,912
9,6437
8,729
5,745
Различные варианты могут быть представлены в виде множества точек
на графике, горизонтальная ось которого – стандартное отклонение, а верти-
кальная ось – математическое ожидание чистой текущей стоимости. Каждая
точка соответствует одной комбинации. Некоторые точки расположены выше
других, так как они представляют проекты с более высоким математическим
ожиданием чистой текущей стоимости и соответствующими стандартными от-
клонениями или с более низким стандартным отклонением и соответствующим
математическим ожиданием чистой текущей стоимости, и с более низким стан-


