119
тоже самое многопериодное бюджетное ограничение, которое было бы при вы-
пуске
у
р
в каждом из периодов:
r
y
y
r
r
y
r
y
y
r
y
y
p
p
p
1
2
1
1
1
2
1
2
1
.
Значение
у
р
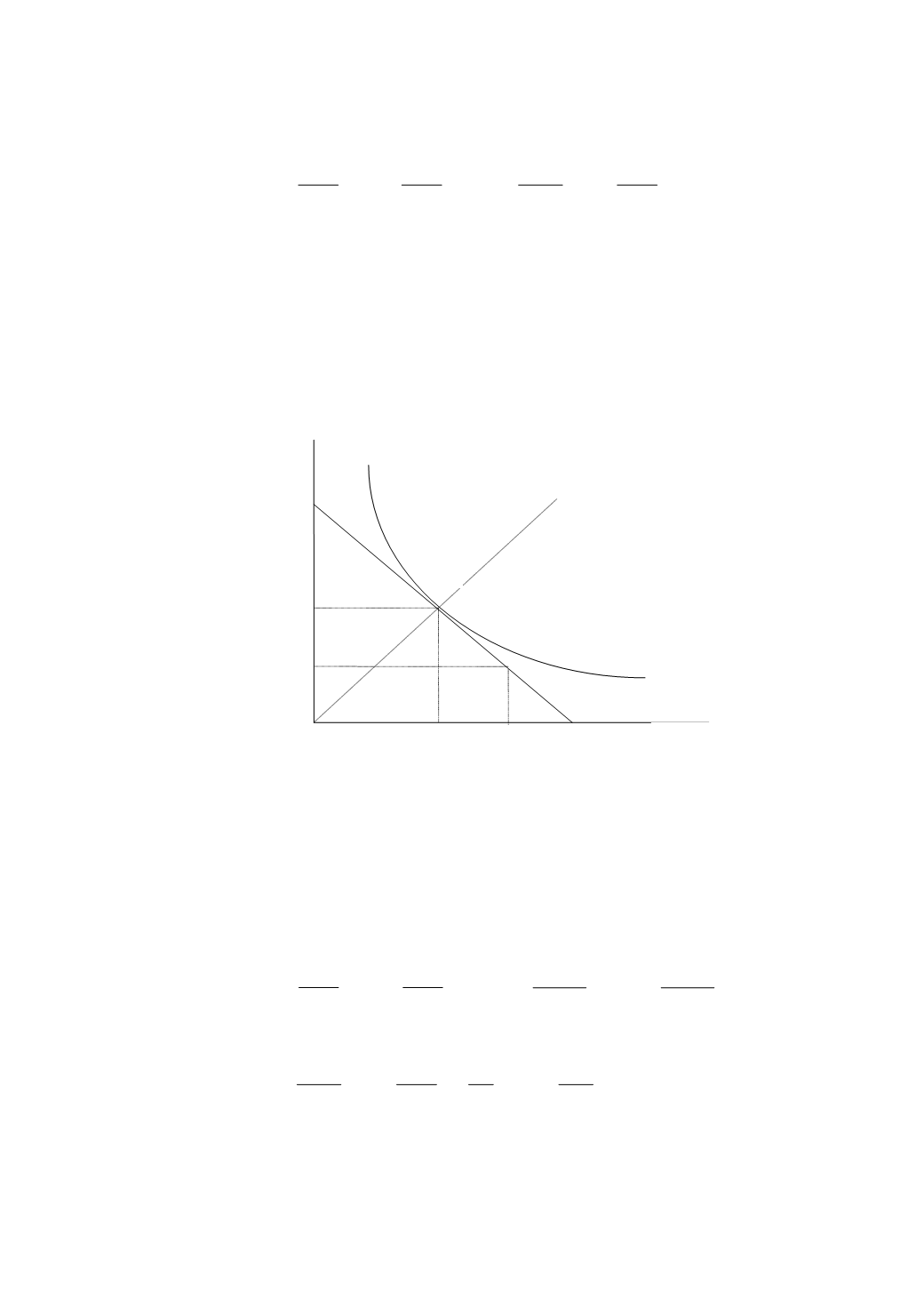
определяется графически пересечением биссектрисы на
плоскости 1-й период – 2-й период с линией бюджетного ограничения (рис. 6.5).
В точке
А
выпуски обоих периодов равны. В данном случае
у
1
> y
p
,
y
2
< у
р
(точка
Е
). Если домашнее хозяйство максимизирует свою полезность, то
в каждом периоде потребление одинаково и равно перманентному доходу
(
С
1
= С
2
= у
р
). Следовательно, сбережения определяются разностью между те-
кущим и постоянным доходом:
S
1
= у
1
– С
1
= у
1
– у
р
.
Рис. 6.5. Потребление и перманентный доход домашнего хозяйства
Пример 2
.
Построить бюджетное ограничение для домашних хозяйств,
которое зарабатывает 100 долларов в первом периоде и 200 долларов во втором
периоде своей жизни. Ставка процента равна 10%. Чему равен перманентный
доход этого домашнего хозяйства?
Решение:
x
r
y
y
r
C
C
1
1
2
1
2
1
,
282
1,0
1
200
100
1,0
1
2
1
C
C
.
Перманентный доход:
8, 147
1,1
200
100
1,2
1,1
1
2
1
2
1
r
y
y
r
r
y
p
.
Период 2
Период 1
C
2
= y
p
C
1
= y
p
y
2
y
1
A
E


