35
Для моментов времени
t
>
t
с
скорость скольжения
( )
0
t
=
u
.
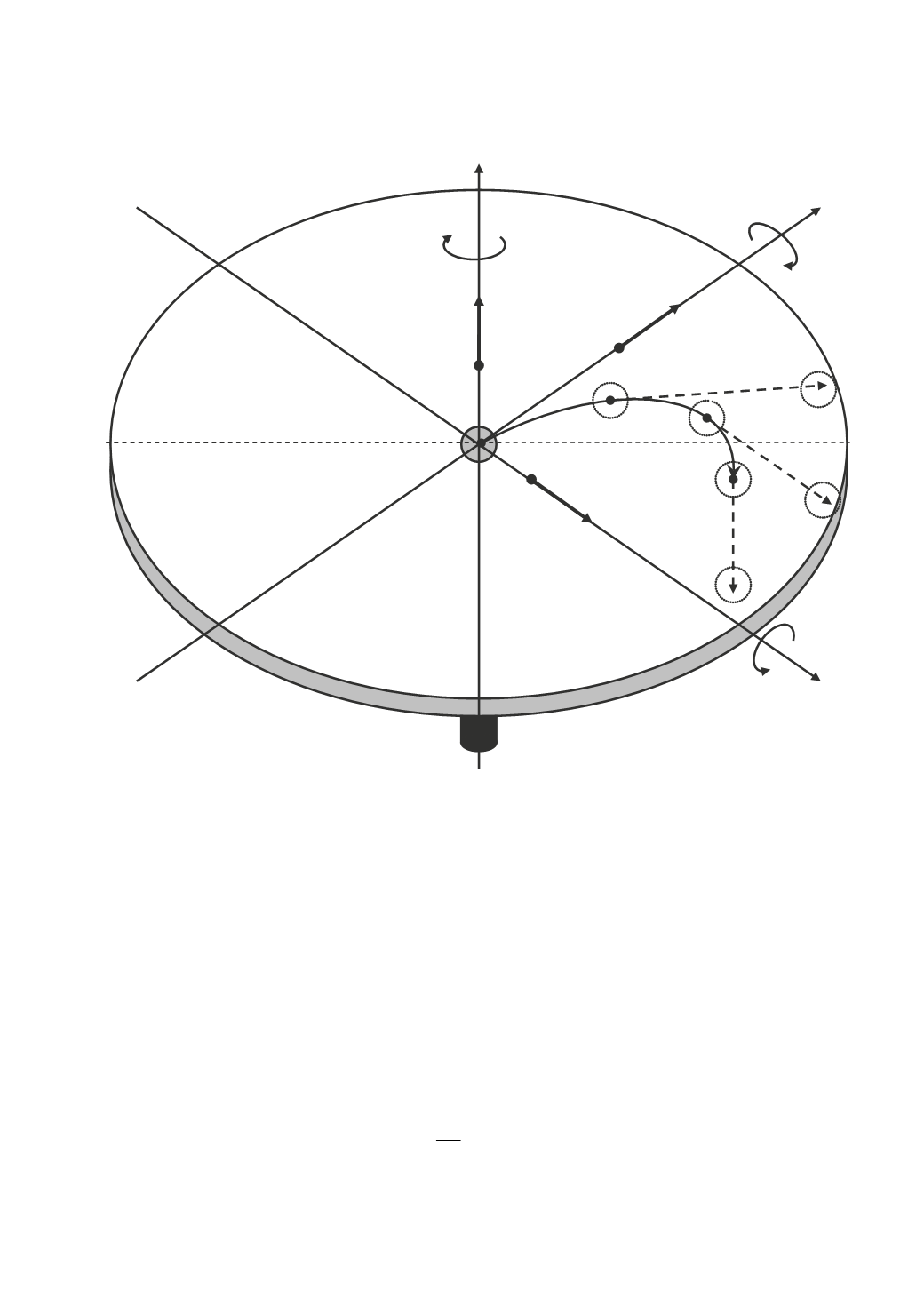
Рис. 15
Уравнения Эйлера (1.31) и (1.32) с учётом (1.30) и (1.36) можно записать в виде
c
f g
′′ =−
r
c
;
(1.39)
(
)
[ ]
ω 5 2 ,
c
f g/ a
e c
′ =
. (1.40)
Вектор ускорения вращательного движения
ω
′
не зависит от времени и пер-
пендикулярен векторам
e
и
c
. Вектор ускорения поступательного движения
′′
r
также не зависит от времени и направлен против постоянного вектора
P
e
.
Сопоставив (1.39) и (1.34), находим, что замедление скольжения и замедление
поступательного движения связаны простым соотношением:
(
)
7 / 2
′
′′
=
u
r
.
Интегрируя (1.39) и (1.40) для интервала времени 0 ≤
t
≤
t
с
, находим
( ) ( ) ( ) ( )
2
0 0 1/ 2
c
t
t
f gt
= + −
r r v
c
, (1.41)
( ) ( )
[ ]
5
ω ω 0
,
2
c
t
f gt
a
= +
e c
. (1.42)
z
y
ω
3
ω
2
e
=
e
z
e
p
=
e
y
=
c
v
(
t
) при
t
0
>
t
c
t
0
>
t
c
t
0
=
t
c
v
(
t
) при
t
0
=
t
c
0
t
0
<
t
c
e
x
v
(
t
) при
t
0
<
t
c
v
(
t
) =
v
1
e
x
+ ((5
v
2
– 2
ω
1
a
)/7)
e
y
ω
1
x


