" Н а у к а м о л о д ы х " , 3 0 - 3 1 м а р т а 2 0 1 7 г . , А р з а м а с
П о с в я щ а е т с я 1 0 0 - л е т и ю Р о с т и с л а в а Е в г е н ь е в и ч а А л е к с е е в а
560
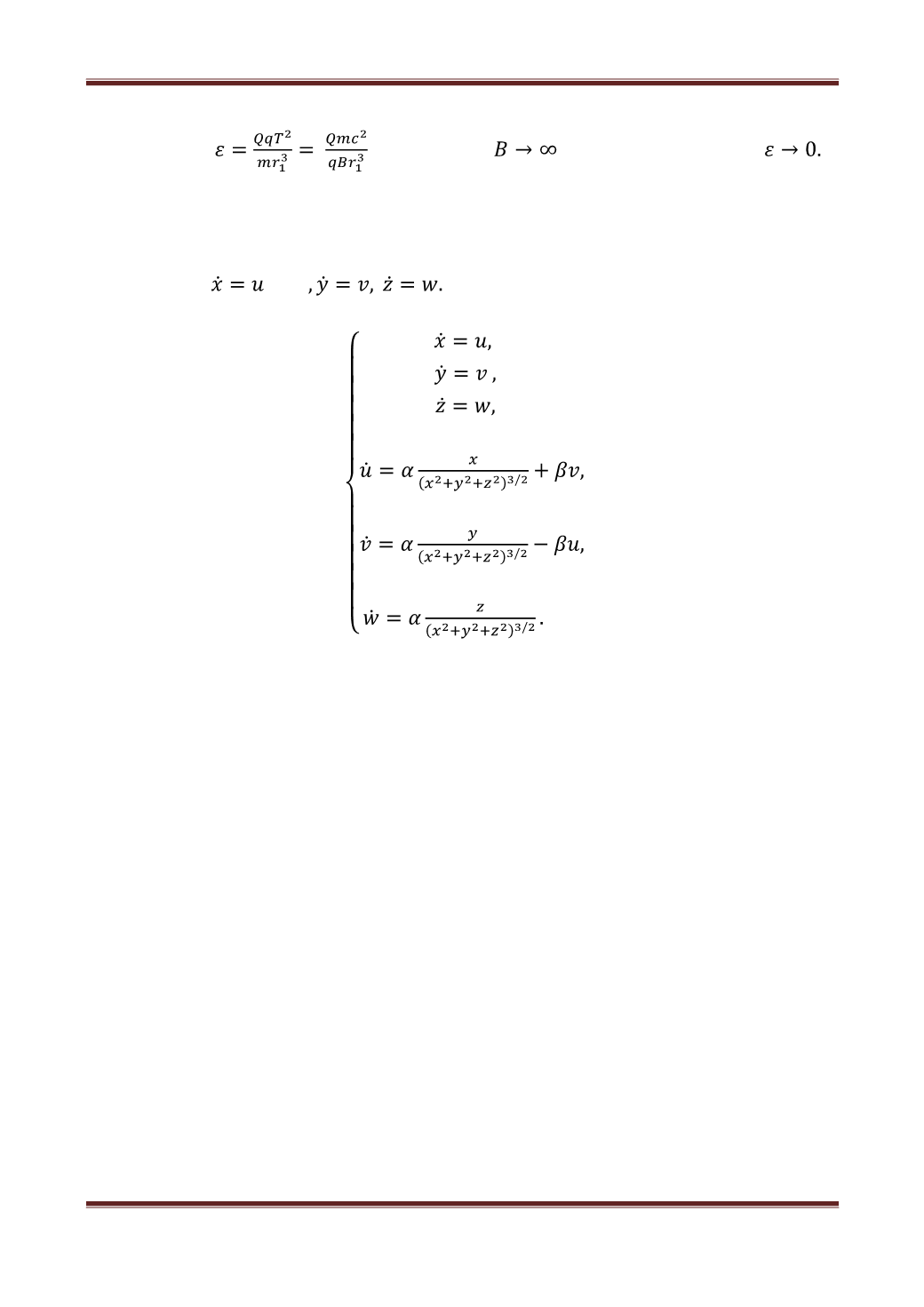
где параметр
при условии
асимптотически мал:
В дальнейших преобразованиях знак «-», стоявший сверху в
обозначениях переменных, для упрощения записи в уравнениях (5) опущен.
Систему уравнений (5) для последующего её численного решения сведём
к системе из шести уравнений первого порядка. Для этого введём
обозначения:
Тогда
(8)
Уравнения (8) проинтегрируем численно при помощи стандартной
программы пакета MatLab. Для этого применим функцию
ode45
, в которой
реализован одношаговый явный метод Рунге-Кутты 4-го порядка с
автоматическим выбором шага интегрирования. Как известно, достаточным
условием применимости этого метода является условие ограниченности правых
частей дифференциальных уравнений вместе с их частными производными
четвёртого порядка [4]. Для системы уравнений (8) это условие заведомо будет
выполнено, если начальные значения функций
x, y, z
заданы в произвольной
области, не содержащей начало координат.
Решение системы уравнений (8) выполнялось для различных значений
параметров
α и β
. Приведём результаты численного расчёта значений функций
x, y, z
на промежутке [0, 500] при α=0,5 и β =1,0 (рисунок).
Вычисления показывают, что координаты
x, y
меняются периодически,
отклоняясь от начальных значений попеременно как влево, так и вправо.
Координата
z
при увеличении времени сначала увеличивается, затем достигает
наибольшей величины и начинает уменьшаться. Это означает, что в
рассматриваемом случае величина кулоновского притяжения между зарядами
достаточно велика для того, чтобы заряженная частица не удалилась от начала
координат в бесконечность, а оставалась в ограниченной области пространства
вблизи начала координат.
Результаты численного интегрирования системы уравнений (8)
согласуются с результатами приближённого решения, полученного нами ранее


