" Н а у к а м о л о д ы х " , 3 0 - 3 1 м а р т а 2 0 1 7 г . , А р з а м а с
П о с в я щ а е т с я 1 0 0 - л е т и ю Р о с т и с л а в а Е в г е н ь е в и ч а А л е к с е е в а
550
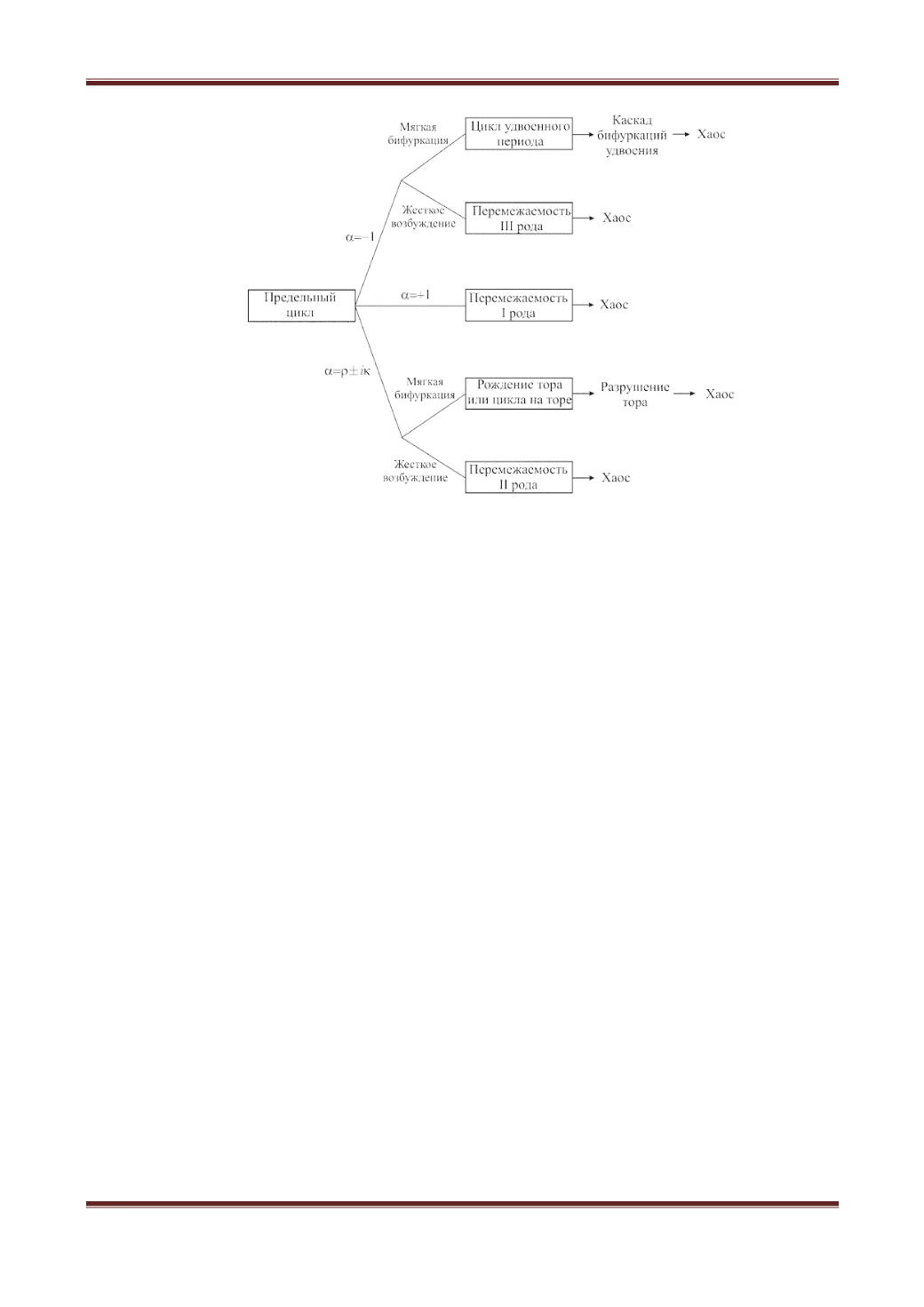
Рис. 1. Типичные бифуркации предельного цикла. Здесь α
собственное значение в пространстве, определяемом секущей
поверхностью
Для того, чтобы система, описываемая системой дифференциальных
уравнений, могла обладать хаотическим режимом, обусловленным странным
аттрактором, число описывающих ее динамических переменных должно быть
не менее трех. Если в такой системе перейти к отображению Пуанкаре, то в нем
фазовые траектории будут представлять собой некоторое множество точек,
нерегулярным образом заполняющих области секущей поверхности. При
сильном сжатии отображение Пуанкаре для многих систем оказывается
близким к одномерному, и поведение фазовых траекторий может быть
приближенно описано одномерным отображением. Когда отображающая точка
такого одномерного отображения долгое время проводит в окрестности начала
координат, для динамической системы это означает, что ее поведениебудет
почти периодическим. Покинув область с почти периодическим движением,
фазовая точка попадает в другую область фазового пространства,
характеризующуюся сложной динамикой. Проведя некоторое время там,
фазовая точка выбрасывается из нее и вновь попадает в ту область фазового
пространства, где происходят почти периодические колебания. При этом
фазовая траектория никогда не замыкается и не уходит в бесконечность.
Описанный режим с перемежаемостью появляется путем слияния устойчивой и
неустойчивой неподвижных точек (через касательную бифуркацию —
перемежаемость I рода). Однако возможны варианты — одновременное
пересечение двух комплексно-сопряженных собственных значений единичной
окружности порождает перемежаемость II рода; при пересечении
действительным собственным значением единичной окружности в точке - 1,


