57
Существуют различные методы расчета тренда. В данном разделе мы
рассмотрим метод
скользящего среднего
, который применяется в том случае,
если ряд содержит явно выраженные сезонные колебания. Пусть исходный ряд
данных (обозначим его
A
i
) содержит
m
экспериментальных точек (1
i
m
).
Известно, что ряд содержит сезонную вариацию с периодом
n
(в нашем приме-
ре
n
= 4). Простейший алгоритм нахождения тренда сводится к поиску значе-
ний тренда в соответствии с формулой
n
j
j i
ni
A
n
F
1
1
1
1
.
Применительно к нашему примеру это означает, что значения тренда
вычисляются по следующим формулам:
F
4
=
(
A
1
+ A
2
+ A
3
+ A
4
)/4;
F
5
=
(
A
2
+ A
3
+ A
4
+ A
5
)/4; … ;
F
16
=
(
A
13
+ A
14
+ A
15
+ A
16
)/4.
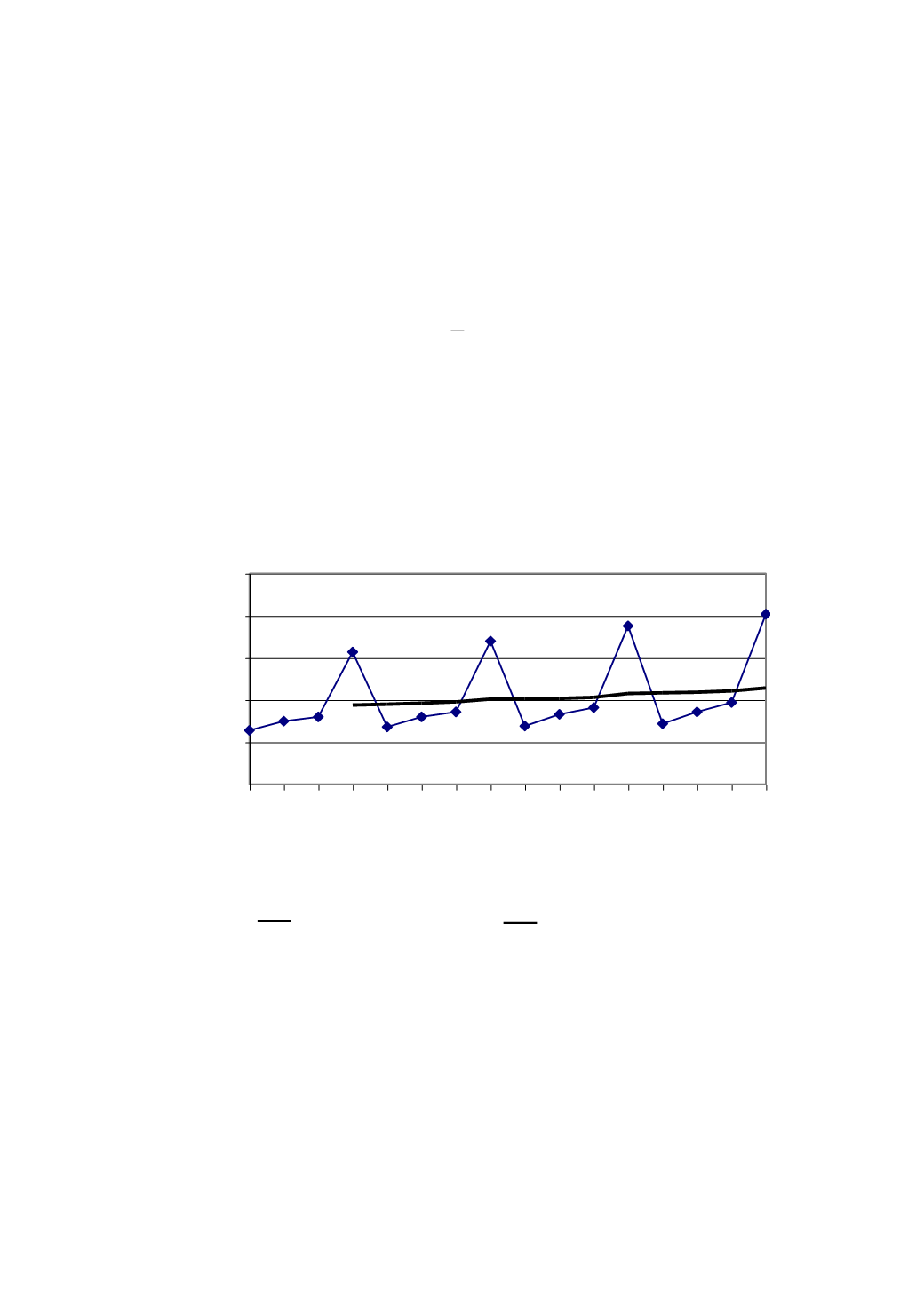
В любом случае будет построена линия тренда (рис.3.19).
Рис. 3.19. Линия тренда:
объем продаж, тыс. р.; линия тренда
Недостатком приведенного алгоритма является не вполне корректная при-
вязка тренда к исходным данным. Действительно, первая точка линии тренда при-
вязана к четвертому периоду, хотя она получается как среднее значение первых
четырех периодов. Более правильно было бы расположить ее между вторым и
третьим периодами, что повысило бы точность окончательного прогноза.
Рассмотрим модернизированный алгоритм скользящего среднего, поз-
воляющий осуществить временную привязку значений тренда к исходному ря-
0
50
100
150
200
250
1997/1
1997/2
1997/3
1997/4
1998/1
1998/2
1998/3
1998/4
1999/1
1999/2
1999/3
1999/4
2000/1
2000/2
2000/3
2000/4


