Модели в инновационной экономике - page 46

44
Спрос на товар зависит от цены товара в данном периоде:
Dt = D(pi ).
Предположим, что функции спроса и предложения линейны, причем
функция предложения имеет положительный, а функция спроса – отрицатель-
ный наклон:
St =  + рt -1, Dt =   pt ,  >  > 0,  > 0,  > 0.
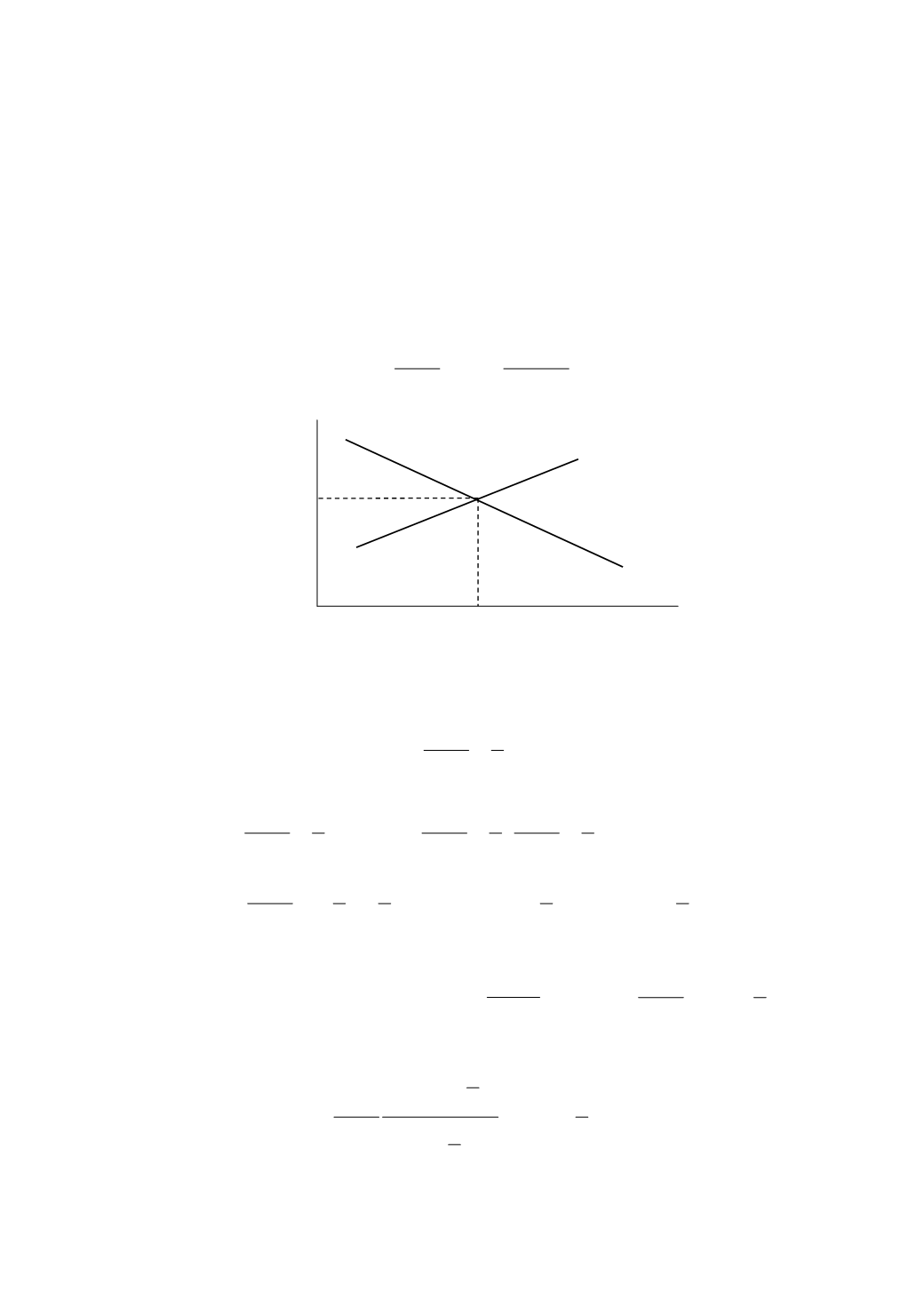
Пересечение прямых спроса и предложения дает равновесные значения
цены и объема выпуска (рис. 3.11).
Q* =   p* = + p* , откуда
.
δβ
βγ αδ
;
δβ
α γ * *





 Q p
Рис. 3.11. Равновесие
Пусть теперь начальная точка не совпадает с равновесной. Выразим pt
через pt-1:
1
δ
β
δ
α γ
 

 t t p p .
Тогда имеем:
    .
δ
β
1
δ
β
1 ...
δ
β
δ
β
1
δ
α γ
...,,
δ
β
δ
αγ
δ
β
δ
αγ
,
δ
β
δ
αγ
0
1
1
2
0 2 0 1
p p
p p p p
n
n
n
n
n 


































 



 




Первое слагаемое есть сумма геометрической прогрессии
 
1
1
... 1 1
1 2
1 

     
q
q
a q q q a S
n
n
n , где .
δ
β
,
δ
α γ
1  

 q a
Тогда в произвольный дискретный момент времени i имеем:
 
  0
δ
β
1
δ
β
1
δ
β
1 1
δ
α γ
p p
i
i
i
i
i 















 .
Проанализируем устойчивость состояния равновесия спроса и предло-
Q*
p*
S
D
p
Q