74
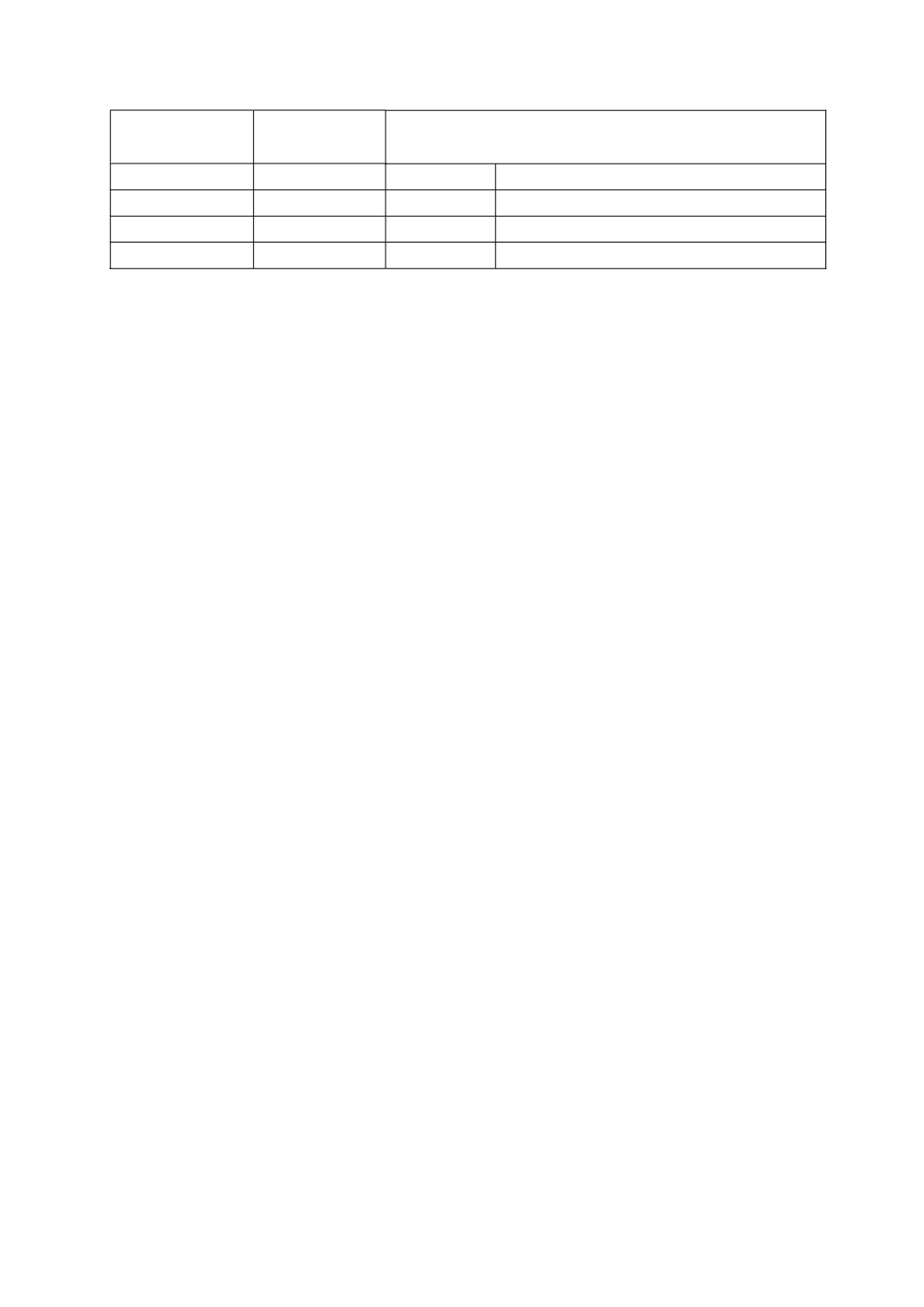
Таблица 4.1
Виды сырья Запас сырья Количество единиц сырья на изготовление
единицы продукции
П
1
П
2
с
1
20
2
5
с
2
40
8
5
с
3
30
5
6
Прибыль от реализации единицы продукции
П
1
составляет 50 руб., а
продукции
П
2
– 40 руб. Необходимо составить такой план выпуска продукции,
чтобы при ее реализации получить максимальную прибыль.
Обозначим через
х
1
количество единиц продукции
П
1
, а через
х
2
– коли-
чество единиц продукции
П
2
. Тогда получим систему ограничений:
2
х
1
+
5
х
2
20; 8
х
1
+
5
х
2
40; 5
х
1
+
6
х
2
30,
которая показывает, что количество сырья, расходуемое на изготовление про-
дукции, не может превысить имеющихся запасов. Конечную цель решаемой за-
дачи - получение максимальной прибыли при реализации продукции – выразим
как функцию двух переменных
х
1
и
х
2
. Реализация
х
1
единиц продукции
П
1
дает
прибыль 50
х
1
, а реализация
х
2
единиц продукции
П
2
дает 40
х
2
руб. прибыли.
Суммарная прибыль
L =
50
х
1
+
40
х
2
.
Необходимо найти такие неотрицательные значения
х
1
и
х
2
, при которых
функция
L
достигает максимума. Условиями не оговорена неделимость едини-
цы продукции, поэтому
х
1
и
х
2
могут быть и дробными числами.
2. Задача о составлении пищевого рациона.
В коммерческой деятель-
ности возникают задачи, связанные с осуществлением рациональных закупок
продуктов, обеспечивающих необходимый рацион питания для поддержания
нормальной жизнедеятельности человека, или формирование диетического пи-
тания в больницах, или задачи составления кормовых смесей на животноводче-
ских фермах. Задачи о рациональном питании решаются в условиях ограничен-
ного ассортимента, товарных запасов, стоимости, суточных норм потребления
питательных веществ и их содержания в продуктах. Причем из всех возможных
вариантов необходимо выбрать самый дешевый.
Рассмотрим пример. Сельскохозяйственное предприятие на промышлен-
ной основе производит откорм бычков (или свиней, уток и т.д.). Для простоты до-
пустим, что имеется два вида продуктов
П
1
и
П
2
. При откорме каждое животное
должно ежедневно получать не менее 9 ед. питательного вещества
С
1
, не менее 8


