267
Формула (9.13) позволит запрограммировать решение системы,
получаемой с помощью неявной разностной схемы, одним из численных
методов, например, с помощью метода Зейделя.
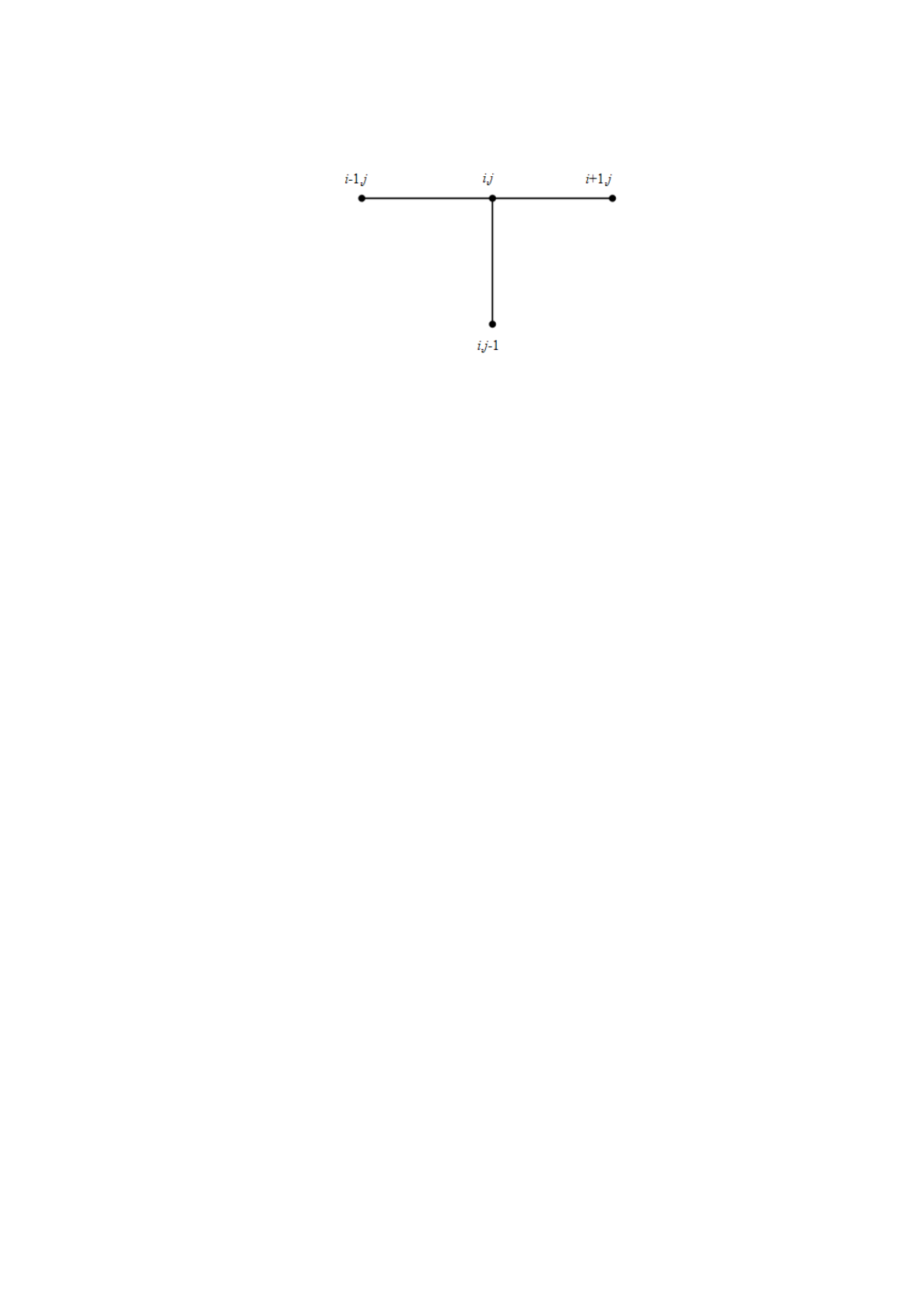
Рис. 9.4. Шаблон неявной двухслойной разностной схемы
Пример 9.2
В данном примере
N
– количество участков, на которые разбивается
интервал по
x
(0,
L
);
K
– количество участков, на которые разбивается
интервал
t
(0,
T
);
а
– параметр дифференциального уравнения
теплопроводности;
eps
– точность решения СЛАУ (9.4) методом Зейделя.
Результатом работы программы является матрица решений
u
для
исходных данных Примера 9.1; массивы
x
,
t
,
r
– точность решения
системы (9.4) методом Зейделя; количество итераций
k
.
Код программы на языке С++:
#include
"iostream"
#include
"math.h"
#include
"fstream"
usingnamespace
std;
//праваячастьдифференциальногоуравнения
double
f(
double
x
,
double
t
)
{
double
y;
y=sin(
x
*
t
);
return
y;
}
//начальноеусловие
double
fi(
double
x
)
{
double
y;
y=exp(0.15*
x
);
return
y;
}
//Условие на левой границе
double
myu(
double
t
)
{
double
y=1;
return
y;
}
//Условие на правой границе
double
nyu(
double
t
)
{
double
y=2.117;
return
y;
}
int
main()
{
double
L,T,a,eps,h,delta,gam,r,k;


